��Ŀ����
����Ŀ���Ķ�������ϣ�
�۲���˼�����Ķ����в��ϣ���������������.�����![]() �У�
��![]() ��
��![]() ��
��![]() �ĶԱ߷ֱ���a��b��c����A��
�ĶԱ߷ֱ���a��b��c����A��![]() ��D����ͼ������
��D����ͼ������![]() ��
��![]() ����
����![]() ��
��![]() ������
������![]() ����
����![]() .ͬ���У�
.ͬ���У�![]() ��
��![]() ������
������![]() .
.
������һ���������У����ߺ������Խǵ����ҵı����.������������У�����֪����Ԫ�أ�������һ���ߣ��������������ۺ��йض����Ϳ��������������δ֪Ԫ��.�����������ϣ�������и���.
��1����ͼ��![]() �У�
��![]() ��
��![]() ��
��![]() ����
����![]() ��
��
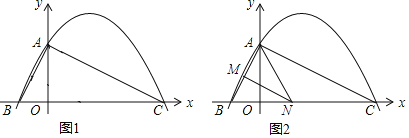
��2����ͼ��һ������C����õ���A�ڻ��ֵı�ƫ��30��ķ����ϣ���������60����/ʱ���ٶȰ���ƫ��30��ķ����У���Сʱ��B������ʱ�ֲ�õ���A�ڻ��ֵı�ƫ��75��ķ����ϣ���ͼ�������ʱ���־����A�ľ���AB.
��3���ڣ�2���������£�����75�������ֵ.������������ţ�

���𰸡���1��20![]() ����2��15
����2��15![]() �����3��
�����3��![]() .
.
��������
��1�����ݲ��ϣ���һ���������У����ߺ������Խǵ����ҵı���ȣ�д��������ϵ��������ֵ�������AB��ֵ.
��2������������ٶȺ�ʱ�����BC�ľ��룬���ɸ�����ǵó���A�ĽǶȣ���B��BM��AC��M�������MBC=30�������MC���ɹ��ɶ������BM�����AM��BM�ij����ɹ��ɶ������AB���ɣ�
��3����������ABC�У���A=45����ABC=75����ACB=60������C��AC�Ĵ���BD������ֱ��������ABD��BCD����ֱ��������ABD�п����AD�ij������������sin75����ֵ��
�⣺��1������ABC�У���B=75������C=45����BC=60�����A=60����
��![]() =
=![]() ��
��
��![]() =
=![]() ��
��
��![]() =
=![]() ��
��
��ã�AB=20![]() .
.
��2����ͼ��

�����⣺BC=60��0.5=30�����
��CD��BE��
���DCB+��CBE=180��
�ߡ�DCB=30����
���CBE=150��
�ߡ�ABE=75����
���ABC=75����
���A=45����
����ABC��![]() =
=![]() ��
��![]() =
=![]() ��
��
��֮�ã�AB=15![]() ��
��
�𣺻��־�����ľ���AB=15![]() ���
���
��3������B��AC�Ĵ���BM������ΪM.
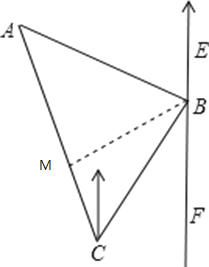
��ֱ��������ABM�У���A=45����AB=15![]() ��
��
����AM=15![]() ����ֱ��������BDC�У���BCM=60����BC=30���������CM=15��
����ֱ��������BDC�У���BCM=60����BC=30���������CM=15��
����AC=15![]() +15��
+15��
������ã�![]() ��
��![]() ��sin75��=
��sin75��=![]() ��
��

 ���б�ˢ��ϵ�д�
���б�ˢ��ϵ�д�����Ŀ����ȥ��������п��У�ijУ6��ѧ���������ɼ�ͳ�����±���
�ɼ� | 17 | 18 | 20 |
���� | 2 | 3 | 1 |
�����й����������ݵ�˵��������ǣ�������
A.������18B.��λ����18C.ƽ������18D.������2
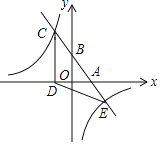
����Ŀ����֪������y��ax2+bx+c(a��0)�ϲ��ֵ�ĺ�����x��������y�Ķ�Ӧֵ���±���
x | �� | ��3 | ��2 | ��1 | 0 | 1 | 2 | 3 | �� |
y | �� |
| ��4 |
| ��4 |
| 0 |
| �� |
(1)��������ߵı���ʽ��
(2)��֪��E(4�� y)�Ǹ��������ϵĵ㣬��E���������ߵĶԳ���ԳƵĵ�Ϊ��F�����E�͵�F�����꣮