题目内容
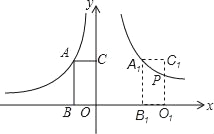
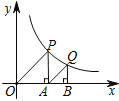
【题目】如图,△OAP与△ABQ均为等腰直角三角形,点P、Q在函数y=![]() (x>0)的图象上,直角顶点A、B均在x轴上,则点B的坐标为__________.
(x>0)的图象上,直角顶点A、B均在x轴上,则点B的坐标为__________.
【答案】(![]() +1,0)
+1,0)
【解析】
若△OAP是等腰直角三角形,那么∠POA=45°,即直线OP:y=x,联立双曲线解析式可求得P(2,2),即A(2,0),然后结合直线OP的斜率求得直线AQ的解析式,联立反比例函数解析式即可得到点Q点坐标,由于B、Q的横坐标相同,即可得出B点的坐标.
∵△OAP是等腰直角三角形,
∴直线OP的解析式为:y=x,
解方程组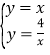 得,
得,
![]() ,
,![]() ,
,
∵点P在第一象限,
∴P(2,2);
∴A(2,0),
∵OP∥AQ,
∴设直线AQ的解析式为:y=x+b,
把A(2,0)代入得,
2+b=0,
解得,b=2,
∴直线AQ的解析式为:y=x2,
解方程组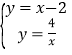 得,
得,
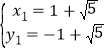 ,
,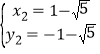 ,
,
∵点Q在第一象限,
∴Q(![]() ,
,![]() ),
),
∴B(![]() ,0).
,0).
故答案为:(![]() +1,0).
+1,0).

练习册系列答案
相关题目