题目内容
【题目】定义:在线段MN上存在点P、Q将线段MN分为相等的三部分,则称P、Q为线段MN的三等分点.
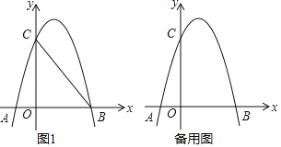
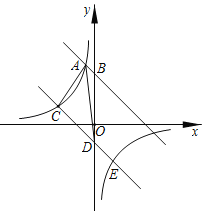
已知一次函数y=﹣x+3的图象与x、y轴分别交于点M、N,且A、C为线段MN的三等分点(点A在点C的左边).
(1)直接写出点A、C的坐标;
(2)①二次函数的图象恰好经过点O、A、C,试求此二次函数的解析式;
②过点A、C分别作AB、CD垂直x轴于B、D两点,在此抛物线O、C之间取一点P(点P不与O、C重合)作PF⊥x轴于点F,PF交OC于点E,是否存在点P使得AP=BE?若存在,求出点P的坐标?若不存在,试说明理由;
(3)在(2)的条件下,将△OAB沿AC方向移动到△O'A'B'(点A'在线段AC上,且不与C重合),△O'A'B'与△OCD重叠部分的面积为S,试求当S=![]() 时点A'的坐标.
时点A'的坐标.

【答案】(1)点A、C的坐标分别为:(1,2)、(2,1);(2)①抛物线的表达式为:y=﹣![]() x2+
x2+![]() x;②P的坐标为:(
x;②P的坐标为:(![]() ,
,![]() );(3)点A′的坐标为:(
);(3)点A′的坐标为:(![]() ,
,![]() )
)
【解析】
(1)先求出M、N的坐标,再根据A、C为线段MN的三等分点,即可求解;
(2)①设函数的表达式为:y=ax2+bx,将点A、C的坐标代入上式即可求解;
②设点P(m,﹣![]() m2+
m2+![]() m),AP=BE,则(m﹣1)2+(﹣
m),AP=BE,则(m﹣1)2+(﹣![]() m2+
m2+![]() m﹣2)2=
m﹣2)2=![]() ,即可求解;
,即可求解;
(3)S=S△A′GK﹣S△A′HR=![]() ×GK×A′K﹣
×GK×A′K﹣![]() HE×A′R=
HE×A′R=![]() (1﹣
(1﹣![]() m)(2﹣m)﹣
m)(2﹣m)﹣![]() (1﹣m)(
(1﹣m)(![]() )=
)=![]() ,即可求解.
,即可求解.
解:(1)一次函数y=﹣x+3的图象与x、y轴分别交于点M、N,令x=0,y=3,则M的坐标为(0,3),令y=0,x=3,则N的坐标为(3,0),由A、C为线段MN的三等分点,则点A、C的坐标分别为:(1,2)、(2,1);
(2)①设函数的表达式为:y=ax2+bx,将点A、C的坐标代入上式得:![]() ,解得:
,解得: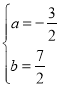 ,
,
故抛物线的表达式为:y=﹣![]() x2+
x2+![]() x;
x;
②存在,理由:
设点P(m,﹣![]() m2+
m2+![]() m),
m),
直线OC的表达式为:y=![]() x,则点B(1,
x,则点B(1,![]() ),BE=
),BE=![]() ,
,
AP=BE,则(m﹣1)2+(﹣![]() m2+
m2+![]() m﹣2)2=
m﹣2)2=![]() ,
,
化简得:7m2﹣15m+7=0,
解得:m=![]() (舍去负值),
(舍去负值),
故点P的坐标为:(![]() ,
,![]() );
);
(3)设直线A′O′交OC于点H,交x轴于点G,直线A′B′交OC于点R,交x轴于点K,过点H作HE⊥A′B′于点E,
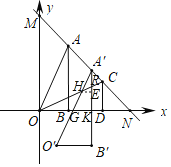
设点A向下平移m个单位向右平移m个单位得到A′(1+m,2﹣m),
设直线O′A′的表达式为:y=2x+b,将点A′的坐标代入上式并解得:
直线O′A′的表达式为:y=2x﹣3m①,
故点G(![]() ,0),则GK=1+m﹣
,0),则GK=1+m﹣![]() =1﹣
=1﹣![]() m,
m,
直线OC的表达式为:y=![]() x②,
x②,
联立①②并解得:x=2m,故点H(2m,m),则HE=1+m﹣2m=1﹣m,
点R(1+m,![]() ),则A′R=2﹣m﹣
),则A′R=2﹣m﹣![]() (m+1)=
(m+1)=![]() ,
,
S=S△A′GK﹣S△A′HR=![]() ×GK×A′K﹣
×GK×A′K﹣![]() HE×A′R=
HE×A′R=![]() (1﹣
(1﹣![]() m)(2﹣m)﹣
m)(2﹣m)﹣![]() ·
·![]() (1﹣m)=
(1﹣m)=![]() ,
,
解得:m=![]() ,
,
故点A′的坐标为:(![]() ,
,![]() ).
).