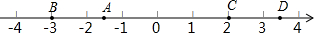题目内容
如图所示,数轴上的点A、B分别表示实数1、
,点C是点B关于点A的对称点,点C表示的实数为x,则代数式x2-4x+3的值为

| 3 |
2
2
.
分析:由于与1、
两个实数对应的点分别为A、B,所以得到AB=
-1,而点C与点B关于点A对称(即AB=AC),由此得到AC=
-1,又A对应的数为1,由此即可求出点C表示的数.
| 3 |
| 3 |
| 3 |
解答:解:∵数轴上与1、
两个实数对应的点分别为A、B,
∴AB=
-1,
而点C与点B关于点A对称(即AB=AC),
∴AC=
-1,
而A对应的数为1,
∴点C表示的数是1-(
-1)=2-
,
x2-4x+3=(2-
)2-4×(2-
)+3=2,
故答案为:2.
| 3 |
∴AB=
| 3 |
而点C与点B关于点A对称(即AB=AC),
∴AC=
| 3 |
而A对应的数为1,
∴点C表示的数是1-(
| 3 |
| 3 |
x2-4x+3=(2-
| 3 |
| 3 |
故答案为:2.
点评:本题考查了实数与数轴的对应关系,同时也利用了关于点对称的性质和数形结合的思想.

练习册系列答案
相关题目
 如图所示,“数轴上的点并不都表示有理数,如图中数轴上的点P所表示的数是
如图所示,“数轴上的点并不都表示有理数,如图中数轴上的点P所表示的数是| 2 |
| A、代入法 | B、换元法 |
| C、数形结合 | D、分类讨论 |
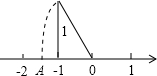 如图所示,数轴上的点A所表示的数为x.则x=
如图所示,数轴上的点A所表示的数为x.则x= 数学魔术:如图所示,数轴上的点A、B、C、D分别表示
数学魔术:如图所示,数轴上的点A、B、C、D分别表示