题目内容
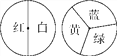
【题目】小明和小亮用如图所示的两个转盘做“配紫色”游戏，游戏规则是：分别转动两个转盘，若其中一个转盘转出红色，另一个转出蓝色，则可以配成紫色，此时小明得1分，否则小亮得1分．
(1)用画树状图或列表的方法求出小明获胜的概率；
(2)这个游戏对双方公平吗？请说明理由．若不公平，如何修改规则才能使游戏对双方公平？
【答案】（1）
（2）不公平
【解析】试题分析：（1）先利用列表法展示所有6种等可能的结果数，再找出可以配成紫色的结果数，然后根据概率公式计算小明获胜的概率；
（2）由于小明获胜的概率和小亮获胜的概率不相等，则可判断游戏不公平，可改为配成紫色小明得5分，否则小亮得1分．
试题解析：(1)列表如下：
黄 | 蓝 | 绿 | |
红 | (红，黄) | (红，蓝) | (红，绿) |
白 | (白，黄) | (白，蓝) | (白，绿) |
总共有6种结果，每种结果出现的可能性相同．其中，可以配成紫色的结果有1种，所以小明获胜的概率为
；
(2)不公平．
理由如下：因为P(配成紫色)＝
，P(没配成紫色)＝
，所以小明P(小明获胜)≠P(小亮获胜)，所以这个游戏对双方不公平．(8分)修改：配成紫色小明得5分，否则小亮得1分．
练习册系列答案
相关题目
