题目内容
关于x的一元二次方程kx2+2x-1=0有两个不相等的实数根,则k的取值范围是 ,若关于x的方程x2-x+cos2α=0有两个相等的实数根,则锐角α为 ,若方程2x(kx-4)-x2+6=0无实数根,则k的最小整数值为 .
【答案】分析:先根据关于x的一元二次方程kx2+2x-1=0有两个不相等的实数根则k≠0,△>0得到关于k的不等式,求出k的取值范围;根据关于x的方程x2-x+cos2α=0有两个相等的实数根可知△=0,由△=0及特殊角的三角函数值可求出α的度数;根据方程2x(kx-4)-x2+6=0无实数根,可得到关于k的不等式,求出k的取值范围.
解答:解:∵关于x的一元二次方程kx2+2x-1=0有两个不相等的实数根,
∴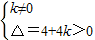 ,解得k>-1且k≠0;
,解得k>-1且k≠0;
∵关于x的方程x2-x+cos2α=0有两个相等的实数根,
∴△=(-1)2-4cos2α=0,解得cosα=± ,
,
∵α为锐角,
∴cosα= ,
,
∵cos60°= ,
,
∴α=60°.
方程2x(kx-4)-x2+6=0可化为(2k-1)x2-8x+6=0
∵此方程无实数根,
∴当2k-1=0,即k= 时-8x+6=0,x=
时-8x+6=0,x= ;
;
当2k-1≠0,即k≠ 时,△=64-24(2k-1)<0,解得k>
时,△=64-24(2k-1)<0,解得k>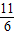 ,
,
∴k的最小整数值为2.
故答案为:k>-1且k≠0;60°;2.
点评:本题考查的是一元二次方程根的判别式及特殊角的三角函数值,熟知一元二次方程根的判别与方程解的关系及特殊角度的三角函数值是解答此题的关键.
解答:解:∵关于x的一元二次方程kx2+2x-1=0有两个不相等的实数根,
∴
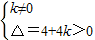 ,解得k>-1且k≠0;
,解得k>-1且k≠0;∵关于x的方程x2-x+cos2α=0有两个相等的实数根,
∴△=(-1)2-4cos2α=0,解得cosα=±
 ,
,∵α为锐角,
∴cosα=
 ,
,∵cos60°=
 ,
,∴α=60°.
方程2x(kx-4)-x2+6=0可化为(2k-1)x2-8x+6=0
∵此方程无实数根,
∴当2k-1=0,即k=
 时-8x+6=0,x=
时-8x+6=0,x= ;
;当2k-1≠0,即k≠
 时,△=64-24(2k-1)<0,解得k>
时,△=64-24(2k-1)<0,解得k>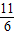 ,
,∴k的最小整数值为2.
故答案为:k>-1且k≠0;60°;2.
点评:本题考查的是一元二次方程根的判别式及特殊角的三角函数值,熟知一元二次方程根的判别与方程解的关系及特殊角度的三角函数值是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目