题目内容
【题目】如图,抛物线y=-![]() x2+
x2+![]() x+
x+![]() 与x轴交于点A,B(点A在点B的左侧),与y轴交于点C.
与x轴交于点A,B(点A在点B的左侧),与y轴交于点C.
(1)求点A,B,C的坐标;
(2)若该抛物线的顶点是点D,求四边形OCDB的面积;
(3)已知点P是该抛物线对称轴的一点,若以点P,O,D为顶点的三角形是等腰三角形,请直接写出点P的坐标.(不用说理)

【答案】(1)点A坐标为(-1,0),点B坐标为(3,0),点C坐标为![]() ;(2)
;(2)![]() ;(3)点P坐标为(1,0)或(1,1+
;(3)点P坐标为(1,0)或(1,1+![]() )或(1,1-
)或(1,1-![]() )或(1,-1).
)或(1,-1).
【解析】
(1)令y=0,可得方程-![]() x2+
x2+![]() x+
x+![]() =0,解方程求得x的值,即可得抛物线与x轴的交点坐标;把x=0代入函数的解析式求得y的值,即可得抛物线与y轴的交点坐标;(2)先求得顶点d的坐标,再由四边形OCDB的面积=△OCD的面积+△OBD的面积即可求得四边形OCDB的面积;(3)分OD=OP、OD=DP和OP=PD三种情况求点P的坐标即可.
=0,解方程求得x的值,即可得抛物线与x轴的交点坐标;把x=0代入函数的解析式求得y的值,即可得抛物线与y轴的交点坐标;(2)先求得顶点d的坐标,再由四边形OCDB的面积=△OCD的面积+△OBD的面积即可求得四边形OCDB的面积;(3)分OD=OP、OD=DP和OP=PD三种情况求点P的坐标即可.
(1)当y=0时,即-![]() x2+
x2+![]() x+
x+![]() =0,
=0,
解得x1=3,x2=-1,
又点A在点B的左侧,
所以点A坐标为(-1,0),点B坐标为(3,0).
当x=0时,y=![]() ,
,
点C坐标为![]() .
.
(2)y=-![]() x2+
x2+![]() x+
x+![]() =-
=-![]() (x-1)2+1,
(x-1)2+1,
所以顶点D的坐标为(1,1),
所以四边形OCDB的面积=△OCD的面积+△OBD的面积=![]() ×1+
×1+![]() ×3×1=
×3×1=![]() .
.
(3)分三种情况:
①当OD=OP时,如图1,
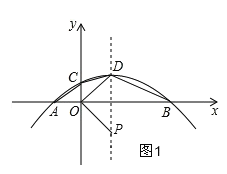
P与D关于x轴对称,
∵D(1,1),
∴P(1,-1),
②当OD=DP时,如图2,
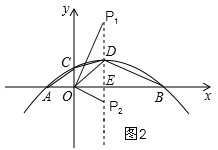
∵D(1,1),
∴OE=DE=1,
∴OD=![]() ,
,
∴PD=OD=![]() ,
,
∴P1(1,1+![]() ),P2(1,1-
),P2(1,1-![]() ),
),
③如图3,
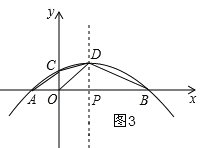
∵D(1,1),
∴当P在x轴上时,OP=PD=1,
∴P(1,0);
综上所述,点P的坐标为:(1,1)或(1,1+![]() )或(1,1-
)或(1,1-![]() )或(1,0).
)或(1,0).

练习册系列答案
相关题目








