Question

【题目】如图，AB是半圆O的直径，点P在BA的延长线上，PD切⊙O于点C，BD⊥PD，垂足为D，连接BC．

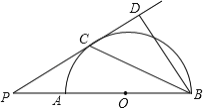
（1）求证：BC平分∠PDB；

（2）求证：BC2=ABBD；

（3）若PA=6，PC=6，求BD的长．

Answer 1

【答案】（1）证明见解析；（2）证明见解析；（3）4．

【解析】

试题分析：（1）连接OC，由PD为圆O的切线，利用切线的性质得到OC垂直于PD，由BD垂直于PD，得到OC与BD平行，利用两直线平行得到一对内错角相等，再由OC=OB，利用等边对等角得到一对角相等，等量代换即可得证；

（2）连接AC，由AB为圆O的直径，利用直径所对的圆周角为直角得到△ABC为直角三角形，根据一对直角相等，以及第一问的结论得到一对角相等，确定出△ABC与△BCD相似，由相似得比例，变形即可得证；

（3）由切割线定理列出关系式，将PA，PC的长代入求出PB的长，由PB-PA求出AB的长，确定出圆的半径，由OC与BD平行得到△PCO与△DPB相似，由相似得比例，将OC，OP，以及PB的长代入即可求出BD的长．

试题解析：（1）连接OC，

∵PD为圆O的切线，

∴OC⊥PD，

∵BD⊥PD，

∴OC∥BD，

∴∠OCB=∠CBD，

∵OC=OB，

∴∠OCB=∠OBC，

∴∠CBD=∠OBC，

则BC平分∠PBD；

（2）连接AC，

∵AB为圆O的直径，

∴∠ACB=90°，

∵∠ACB=∠CDB=90°，∠ABC=∠CBD，

∴△ABC∽△CBD，

∴，即BC2=ABBD；

（3）∵PC为圆O的切线，PAB为割线，

∴PC2=PAPB，即72=6PB，

解得：PB=12，

∴AB=PB-PA=12-6=6，

∴OC=3，PO=PA+AO=9，

∵△OCP∽△BDP，

∴，即，

则BD=4．