题目内容
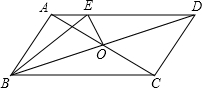如图，在周长为18cm的平行四边形中，AC，BD相交于点O，OE⊥BD交AD与E，则△ABE的周长为
- A.6cm
- B.7cm
- C.8cm
- D.9cm
D
分析：根据平行四边形的性质可知，平行四边形的对边相等，已知周长，可以求出AB+AD的和，由中垂线的性质可知，BE=DE，所以△ABE的周长=AB+AE+BE=AB+AD．
解答：∵平行四边形的周长为18cm
∴AB+AD=9cm
又AC、BD互相平分，且OE⊥BD
∴BE=DE
∴△ABE的周长=AB+AD=9cm
故选D．
点评：此题结合线段垂直平分线的性质，考查了平行四边形的性质，解题的关键是将三角形的三边长转化为平行四边形的一组邻边的长．
分析：根据平行四边形的性质可知，平行四边形的对边相等，已知周长，可以求出AB+AD的和，由中垂线的性质可知，BE=DE，所以△ABE的周长=AB+AE+BE=AB+AD．
解答：∵平行四边形的周长为18cm
∴AB+AD=9cm
又AC、BD互相平分，且OE⊥BD
∴BE=DE
∴△ABE的周长=AB+AD=9cm
故选D．
点评：此题结合线段垂直平分线的性质，考查了平行四边形的性质，解题的关键是将三角形的三边长转化为平行四边形的一组邻边的长．
练习册系列答案
相关题目
如图，在△ABC中，CF⊥AB于F，BE⊥AC于E，M为BC的中点，EF=5，BC=8，则△EFM的周长是（ ）| A、13 | B、18 | C、15 | D、21 |
3、如图，在菱形ABCD中，对角线AC=4，∠BAD=120°，则菱形ABCD的周长为（ ）
如图，在菱形ABCD中，对角线AC与BD相交于点O，AC=6，BD=8，将△AOB沿射线AD的方向平移，平移的距离为线段AD的长，平移后得△DEC，则四边形ACED的周长等于（ ）
如图，在△ABC中，AC的垂直平分线ED交AC于点E，交AB与点D，CE=4，△BCD的周长等于12，则△ABC的周长为（ ）
如图，在?ABCD中，EF过对角线的交点O，AB=4，AD=5，OF=2，则四边形BAEF的周长为（ ）