题目内容
【题目】如图,在平面直角坐标系xOy中,点C的坐标为(4,0),一次函数![]() 的图像分别交x轴、y轴于点A、点B.
的图像分别交x轴、y轴于点A、点B.
⑴ 若点D是直线AB在第一象限内的点,且BD=BC,试求出点D的坐标.
⑵ 在⑴的条件下,若点Q是坐标轴上的一个动点,试探索在第一象限是否存在另一个点P,使得以B、D、P、Q为顶点的四边形是菱形(BD为菱形的一边)?若存在,请直接写出点P的坐标;若不存在,请说明理由.
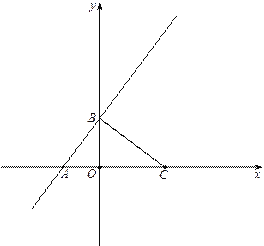
【答案】(1)点D 的坐标为(3,7)
(2)点P的坐标为(3,12)或(3,2)或(7,4)
【解析】试题分析:(1)先求出OB=3,进而求出BC=5,再用勾股定理建立方程求出点D;
(2)分点Q在y轴和x轴,两种情况讨论,先利用菱形的性质求出BQ=5进而得出点Q的坐标,再利用菱形的对边平行即可求出点P的坐标.
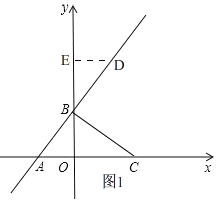
试题解析:(1)如图1,设点D(3a,4a+3),
过点D作DE⊥y轴于E,把x=0代入y=![]() x+3中,得,y=3,
x+3中,得,y=3,
∴OB=3,
∴BE=OE-OB=4a+3-3=4a,BC=![]() =5,
=5,
在Rt△BED中,根据勾股定理得,(3a)2+(4a)2=52,
∴a=±1,
∵点D在第一象限,
∴a=1,
∴D(3,7);
(2)由(1)知,BD=BC=5,
①当点Q在y轴上时,
设Q(0,q),
∵使得以B,D,P,Q为顶点的四边形是菱形(BD为菱形的一边),且点P在第一象限内,
即:四边形BDPQ是菱形,
∴PQ∥BD,DP∥BQ,
∴点P的横坐标为3,
∵四边形BDPQ是菱形,
∴BQ=BD=5,
∵B(0,3),
∴Q(0,8)或(0,-2),
Ⅰ、当点Q(0,8)时,
∵直线BD的解析式为y=![]() x+3,
x+3,
∴直线PQ的解析式为y=![]() x+8,
x+8,
当x=3时,y=12,
∴P(3,12),
Ⅱ、点Q(0,-2)时,
∵直线BD的解析式为y=![]() x+3,
x+3,
∴直线PQ的解析式为y=![]() x-2,
x-2,
当x=3时,y=2,
∴P(3,2),
②当点Q在x轴上时,
设Q(m,0),),
∵使得以B,D,P,Q为顶点的四边形是菱形(BD为菱形的一边),且点P在第一象限内,
即:四边形BDPQ是菱形,
∴BQ=BD=5,
∵OB=3,
∴OQ=4,
∴Q(-4,0)或(4,0)
Ⅰ、当Q(-4,0)时,∵一次函数y=![]() x+3的图象交x轴于点A,
x+3的图象交x轴于点A,
∴A(-![]() ,0),
,0),
∴点Q在点A的左侧,
∴点P在第二象限内,不符合题意,舍去,
Ⅱ、当点Q(4,0)时,∵四边形BDPQ是菱形,
∴BQ∥DP,PQ∥BD,
∵直线BD的解析式为y=![]() x+3,
x+3,
∴设直线PQ的解析式为y=![]() x+b,
x+b,
∴![]() ×4+b=0,
×4+b=0,
∴b=-![]() ,
,
∴直线PQ的解析式为y=![]() x-
x-![]() ①,
①,
∵B(0,3),Q(4,0),
∴直线BQ的解析式为y=-![]() x+3,
x+3,
∵D(3,7),
∴直线DP的解析式为y=-![]() x+
x+![]() ②,
②,
联立①②解得,x=7,y=4,
∴P(7,4),
即:满足条件的点P的坐标为(3,12)、(3,2)、(7,4).

 阅读快车系列答案
阅读快车系列答案