题目内容
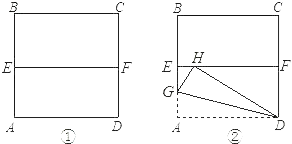
【题目】有一边长为2的正方形纸片ABCD,先将正方形ABCD对折,设折痕为EF(如图①);再沿过点D的折痕将角A翻折,使得点A落在EF的H上(如图②),折痕交AE于点G,则EG的长度为( )
A. 4![]() ﹣6 B. 2
﹣6 B. 2![]() ﹣3 C. 8﹣4
﹣3 C. 8﹣4![]() D. 4﹣2
D. 4﹣2![]()
【答案】B
【解析】
由于正方形纸片ABCD的边长为2,所以将正方形ABCD对折后AE=DF=1,由翻折不变性的原则可知AD=DH=2,AG=GH,在Rt△DFH中利用勾股定理可求出HF的长,进而求出EH的长,再设EG=x,在Rt△EGH中,利用勾股定理即可求解.
∵正方形纸片ABCD的边长为2,
∴将正方形ABCD对折后AE=DF=1,
∵△GDH是△GDA沿直线DG翻折而成,
∴AD=DH=2,AG=GH,
在Rt△DFH中,
HF= ![]() ,
,
∴EH=2-![]() ,
,
在Rt△EGH中,设EG=x,则GH=AG=1-x,
∴GH2=EH2+EG2,
即(1-x)2=(2-![]() )2+x2,
)2+x2,
解得x=2![]() -3.
-3.
故选:B.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
【题目】有这样一个问题:探究函数y=![]() 的图象与性质.小彤根据学习函数的经验,对函数y=
的图象与性质.小彤根据学习函数的经验,对函数y=![]() 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小彤探究的过程,请补充完整:
(1)函数y=![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
(2)下表是y与x的几组对应值:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | 4 | 5 | 6 | 7 | 8 | … |
y | … |
| m |
| 0 | ﹣1 | 3 | 2 |
|
|
| … |
则m的值为 ;
(3)如图所示,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出了图象的一部分,请根据剩余的点补全此函数的图象;
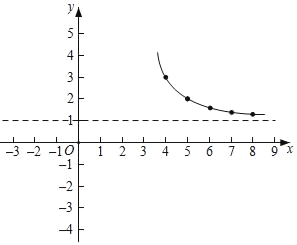
(4)观察图象,写出该函数的一条性质 ;
(5)若函数y=![]() 的图象上有三个点A(x1,y1)、B(x2,y2)、C(x3,y3),且x1<3<x2<x3,则y1、y2、y3之间的大小关系为 ;
的图象上有三个点A(x1,y1)、B(x2,y2)、C(x3,y3),且x1<3<x2<x3,则y1、y2、y3之间的大小关系为 ;