题目内容
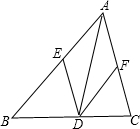
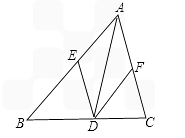
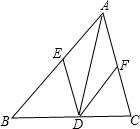已知如图所示，AD是△ABC的角平分线，DE∥AC交AB于E，DF∥AB交AC于F，四边形AEDF是菱形吗？说明理由．
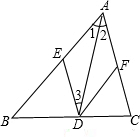解：如图，由于DE∥AC，DF∥AB，所以四边形AEDF为平行四边形．∵DE∥AC，∴∠3=∠2，
又∠1=∠2，∴∠1=∠3，
∴AE=DE，∴平行四边形AEDF为菱形．
分析：先判定四边形AEDF是平行四边形，然后再推出一组邻边相等．
点评：此题运用了菱形的判定方法“一组邻边相等的平行四边形是菱形”．
练习册系列答案
名校课堂系列答案
相关题目
26、已知如图所示，AD是△ABC的角平分线，DE∥AC交AB于E，DF∥AB交AC于F，四边形AEDF是菱形吗？说明理由．
