题目内容
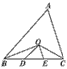
 17、如图所示,BO平分∠CBA,CO平分∠ACB,过O作EF∥BC,若AB=12,AC=18,则△AEF的周长为
17、如图所示,BO平分∠CBA,CO平分∠ACB,过O作EF∥BC,若AB=12,AC=18,则△AEF的周长为30
.分析:由角平分线以及平行线的性质可以得到等角,从而可以判定△OEB和△OFC是等腰三角形,△AEF的周长被转化为△ABC的两边AB和AC的和,即求得△AEF的周长为30.
解答:解:∵BO平分∠CBA,
∴∠EBO=∠OBC,
∵CO平分∠ACB,
∴∠FCO=∠OCB,
∵EF∥BC,
∴∠EOB=∠OBC,∠FOC=∠OCB,
∴∠EBO=∠EOB,∠FOC=∠FCO,
∴BE=OE,CF=OF,
∴△AEF的周长AE+OE+OF+AF=AE+BE+CF+AF=AB+AC,
∵AB=12,AC=18,
∴C△AEF=12+18=30.
∴∠EBO=∠OBC,
∵CO平分∠ACB,
∴∠FCO=∠OCB,
∵EF∥BC,
∴∠EOB=∠OBC,∠FOC=∠OCB,
∴∠EBO=∠EOB,∠FOC=∠FCO,
∴BE=OE,CF=OF,
∴△AEF的周长AE+OE+OF+AF=AE+BE+CF+AF=AB+AC,
∵AB=12,AC=18,
∴C△AEF=12+18=30.
点评:本题利用角平分线和平行线的性质,得到等角,进而得到等腰三角形,通过等边的转化,将△AEF的周长转化为已知条件AB,AC的和,使问题得以解决,题目典型,难度中等.

练习册系列答案
相关题目
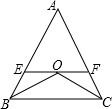 如图所示,BO平分∠CBA,CO平分∠ACB,过O作EF∥BC,若△AEF的周长为12,则AB+AC等于
如图所示,BO平分∠CBA,CO平分∠ACB,过O作EF∥BC,若△AEF的周长为12,则AB+AC等于 如图所示,BO平分∠CBA,CO平分∠ACB,过O作EF∥BC,若AB=12,AC=18,则△AEF的周长为________.
如图所示,BO平分∠CBA,CO平分∠ACB,过O作EF∥BC,若AB=12,AC=18,则△AEF的周长为________.