题目内容
如图所示, BO、CO分别平分△ABC的内角∠ABC、∠ACB,OD∥AB,OE∥AC。若BC=13cm,求△ODE的周长。
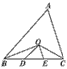
解:∵OB平分∠ABC
∴∠ABO=∠CBO
∵OD∥AB
∴∠ABO=∠BOD
∴∠CBO=∠BOD
∴OD=BD
同理,OE=EC
∴△ODE的周长=OD+OE+DE=BD+DE+EC=BC=13(cm)。
∴∠ABO=∠CBO
∵OD∥AB
∴∠ABO=∠BOD
∴∠CBO=∠BOD
∴OD=BD
同理,OE=EC
∴△ODE的周长=OD+OE+DE=BD+DE+EC=BC=13(cm)。

练习册系列答案
相关题目
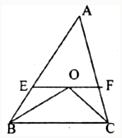 17、如图所示,BO平分∠CBA,CO平分∠ACB,过O作EF∥BC,若AB=12,AC=18,则△AEF的周长为
17、如图所示,BO平分∠CBA,CO平分∠ACB,过O作EF∥BC,若AB=12,AC=18,则△AEF的周长为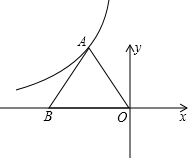
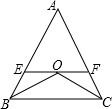 如图所示,BO平分∠CBA,CO平分∠ACB,过O作EF∥BC,若△AEF的周长为12,则AB+AC等于
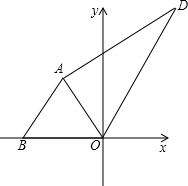
如图所示,BO平分∠CBA,CO平分∠ACB,过O作EF∥BC,若△AEF的周长为12,则AB+AC等于 (x<0)经过点A.
(x<0)经过点A.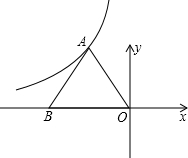
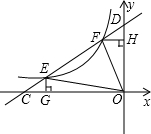
 与x轴,y轴交于C,D两点,与(1)中的反比例函数的图象交于E,F两点,EG⊥x轴于G点,FH⊥y轴于H点,若△DFH的面积记为S△DFH,已知S△DFH+S△FOE+S△ECG=
与x轴,y轴交于C,D两点,与(1)中的反比例函数的图象交于E,F两点,EG⊥x轴于G点,FH⊥y轴于H点,若△DFH的面积记为S△DFH,已知S△DFH+S△FOE+S△ECG= S△COD,求k的值;
S△COD,求k的值;
