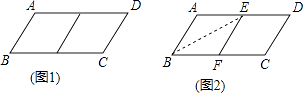题目内容
【题目】已知四边形ABCD是正方形,点E、F分别在边AB、边BC上,DE⊥AF,DE与AF交于点O,将线段AE沿AF进行平移至FG,过点G作GH⊥AB的延长线于点H.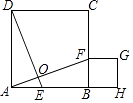
(1)判断四边形BFGH的形状并证明;
(2)写出图中所有面积相等的图形.
【答案】
(1)解:∵四边形ABCD是正方形,
∴AD=AB,∠DAE=∠ABC=90°,
∵DE⊥AF,
∴∠AOE=90°,
∴∠BAF+∠AEO=90°,∠AEO+∠ADE=90°,
∴∠ADE=∠BAD,
在△ADE和△BAF中,
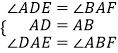 ,
,
∴△ADE≌△BAD,
∴AE=BF,
∵AE=FG,
∴BF=FG,
∵GH⊥AH,FB⊥AH,
∴FB∥GH,
∵FG∥BH,
∴四边形BFGH是平行四边形,
∵∠FBH=90°,
∴四边形BFGH是矩形,
∵FG=BF,
∴四边形BFGH是正方形.
(2)解:图中所有面积相等的图形有:△ADE和△ABF,△ADO和四边形EBFOD的面积相等.
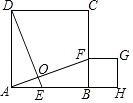
【解析】(1)由平移的性质和正方形的性质可证出△ADE≌△BAF,AE=FG=BF,进而证出四边形BFGH是正方形;(2)由△ADE≌△BAF,可得出它们面积相等,同时减去△AOE的面积,得到△ADO和四边形EBFOD的面积相等.
【考点精析】解答此题的关键在于理解正方形的性质的相关知识,掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形,以及对平移的性质的理解,了解①经过平移之后的图形与原来的图形的对应线段平行(或在同一直线上)且相等,对应角相等,图形的形状与大小都没有发生变化;②经过平移后,对应点所连的线段平行(或在同一直线上)且相等.