Question

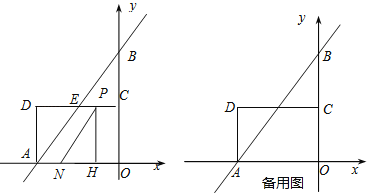
【题目】如图，正方形AOCB的边长为4，反比例函数的图象过点E（3，4）．

（1）求反比例函数的解析式；

（2）反比例函数的图象与线段BC交于点D，直线过点D，与线段AB相交于点F，求点F的坐标；

（3）连接OF，OE，探究∠AOF与∠EOC的数量关系，并证明．

Answer 1

【答案】（1）y=；（2）（2，4）．（3）∠AOF=∠EOC．见解析

【解析】

试题分析：（1）设反比例函数的解析式为y=，把点E（3，4）代入即可求出k的值，进而得出结论；

（2）由正方形AOCB的边长为4，故可知点D的横坐标为4，点F的纵坐标为4．由于点D在反比例函数的图象上，所以点D的纵坐标为3，即D（4，3），由点D在直线y=﹣x+b上可得出b的值，进而得出该直线的解析式，再把y=4代入直线的解析式即可求出点F的坐标；

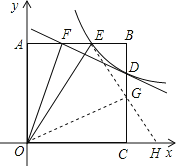
（3）在CD上取CG=AF=2，连接OG，连接EG并延长交x轴于点H，由全等三角形的判定定理可知△OAF≌△OCG，△EGB≌△HGC（ASA），故可得出EG=HG．设直线EG的解析式为y=mx+n，把E（3，4），G（4，2）代入即可求出直线EG的解析式，故可得出H点的坐标，在Rt△AOF中，AO=4，AE=3，根据勾股定理得OE=5，可知OH=OE，即OG是等腰三角形底边EF上的中线．所以OG是等腰三角形顶角的平分线，由此即可得出结论．

解：（1）设反比例函数的解析式y=，

∵反比例函数的图象过点E（3，4），

∴4=，即k=12．

∴反比例函数的解析式y=；

（2）∵正方形AOCB的边长为4，

∴点D的横坐标为4，点F的纵坐标为4．

∵点D在反比例函数的图象上，

∴点D的纵坐标为3，即D（4，3）．

∵点D在直线y=﹣x+b上，

∴3=﹣×4+b，解得b=5．

∴直线DF为y=﹣x+5，

将y=4代入y=﹣x+5，得4=﹣x+5，解得x=2．

∴点F的坐标为（2，4）．

（3）∠AOF=∠EOC．

证明：在CD上取CG=AF=2，连接OG，连接EG并延长交x轴于点H．

∵AO=CO=4，∠OAF=∠OCG=90°，AF=CG=2，

∴△OAF≌△OCG（SAS）．

∴∠AOF=∠COG．

∵∠EGB=∠HGC，∠B=∠GCH=90°，BG=CG=2，

∴△EGB≌△HGC（ASA）．

∴EG=HG．

设直线EG：y=mx+n，

∵E（3，4），G（4，2），

∴，解得，．

∴直线EG：y=﹣2x+10．

令y=﹣2x+10=0，得x=5．

∴H（5，0），OH=5．

在Rt△AOE中，AO=4，AE=3，根据勾股定理得OE=5．

∴OH=OE．

∴OG是等腰三角形底边EH上的中线．

∴OG是等腰三角形顶角的平分线．

∴∠EOG=∠GOH．

∴∠EOG=∠GOC=∠AOF，即∠AOF=∠EOC．