题目内容
如图，△AFC≌△DEB且AF=DE，下列结论不正确的是（ ）
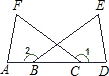
| A．∠1=∠2 | B．AC=DB | C．AB=DC | D．∠E=∠A |
∵△AFC≌△DEB，AF=DE，
∴∠ACF=∠DBE，∠F=∠E，∠A=∠D，
又∵∠1=∠A+∠F，∠2=∠E+∠D，
∴∠1=∠2，
∵AC=DB，
即AB+BC=BC+CD，
∴AB=CD，
由以上分析，可知A、B、C均合题意，
∠E与∠A不是对应角，二者不一定相等
∴D不正确．
故选D．
∴∠ACF=∠DBE，∠F=∠E，∠A=∠D，
又∵∠1=∠A+∠F，∠2=∠E+∠D，
∴∠1=∠2，
∵AC=DB，
即AB+BC=BC+CD，
∴AB=CD，
由以上分析，可知A、B、C均合题意，
∠E与∠A不是对应角，二者不一定相等
∴D不正确．
故选D．
练习册系列答案
相关题目
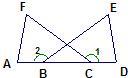6、如图，△AFC≌△DEB且AF=DE，下列结论不正确的是（ ）
4、如图，在平行四边形ABCD中，F是AD上的一点，CF=CD，若∠B=72°，则∠AFC的度数是（ ）
如图，已知AB∥CD，EF分别交AB、CD于点E、F，FB是∠EFD的平分线，AF⊥FB，∠AEF=68°．试求∠AFC的度数．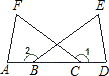
如图，△AFC≌△DEB且AF=DE，下列结论不正确的是