题目内容
线段AB与CD交于点O，若AB=3AO，则当CO：DO的值为分析：根据AC∥BD，即可证明∠OBD=∠OAC，进而可以证明△AOC∽△BOD，即可以求得
=
，即可解题．
| AO |
| BO |
| CO |
| DO |
解答：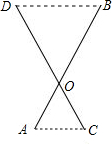
解：∵AC∥BD∴∠OBD=∠OAC，
∵∠AOC=∠BOD，∴△AOC∽△BOD，
∴
=
，
∵AB=3AO，
∴
=
．
故答案为
．
解：∵AC∥BD∴∠OBD=∠OAC，∵∠AOC=∠BOD，∴△AOC∽△BOD，
∴
| AO |
| BO |
| CO |
| DO |
∵AB=3AO，
∴
| CO |
| DO |
| 1 |
| 2 |
故答案为
| 1 |
| 2 |
点评：本题考查了平行线定理，相似三角形的证明，相似三角形对应边比值相等的性质，本题中求证△AOC∽△BOD是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
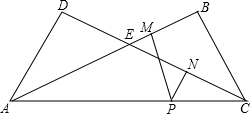如图，将矩形纸片ABCD沿对角线AC折叠，AB与CD交于点E．
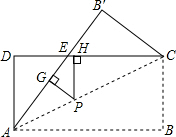如图，将矩形纸片ABCD沿其对角线AC折叠，使点B落到点B′的位置，AB′与CD交于点E．