题目内容
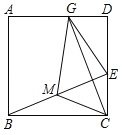
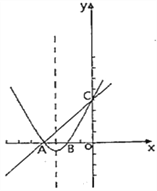
【题目】如图 ,∠E=∠F=90°,∠B=∠C,AC=AB,给出下列结论:① ∠1=∠2;② BE=CF;③ △ACN≌△ABM;④ CD=DN,其中正确的结论有( )个

A.1B.2C.3D.4
【答案】C
【解析】
①由∠E=∠F=90°、∠B=∠C,利用等角的余角相等可得出∠1=∠2,结论①正确;②由∠B=∠C、∠E=∠F、AE=AF,即可证出△BAE≌△CAF(AAS),根据全等三角形的性质可得出BE=CF,结论②正确;③由△BAE≌△CAF可得出AB=AC,结合∠C=∠B、∠CAN=∠BAM即可证出△ACN≌△ABM(ASA),结论③正确;④通过证△BDN≌△CDM可得出DN=DM,根据三角形外角的性质结合等腰三角形的性质即可得出CD≠DN,结论④错误.综上即可得出结论.
解:①∵∠E=∠F=90°,∠B=∠C,
∴∠BAE=∠CAF,
∵∠BAE=∠BAC+∠2,∠CAF=∠CAB+∠1,
∴∠1=∠2,结论①正确;
②在△BAE和△CAF中,
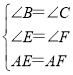
∴△BAE≌△CAF(AAS),
∴BE=CF,结论②正确;
③∵△BAE≌△CAF,
∴AB=AC.
在△ACN和△ABM中,
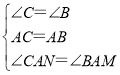 ,
,
∴△ACN≌△ABM(ASA),结论③正确;
④∵△ACN≌△ABM,
∴AN=AM.
∵AB=AC,
∴BN=CM.
在△BDN和△CDM中,
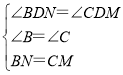 ,
,
∴△BDN≌△CDM(AAS),
∴DN=DM.
∵∠CMD=∠CAB+∠B,∠C=∠B,
∴∠CMD≠∠C,
∴CD≠DM,
∴CD≠DN,结论④错误.
故选:C.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目