题目内容
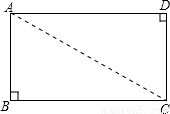
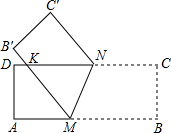 如图,矩形纸片ABCD,AD=BC=3,AB=CD=9,在矩形ABCD的边AB上取一点M,在CD上取一点N,将纸片沿MN折叠,使MB与DN交于点K,得到△MNK,以下命题:
如图,矩形纸片ABCD,AD=BC=3,AB=CD=9,在矩形ABCD的边AB上取一点M,在CD上取一点N,将纸片沿MN折叠,使MB与DN交于点K,得到△MNK,以下命题:①△MNK一定是等腰三角形;
②△MNK可能是钝角三角形;
③△MNK有最小面积且等于4.5;
④△MNK有最大面积且7.5,
其中对△MNK的叙述正确的为
①②③④
①②③④
.分析:①首先根据矩形的性质可得AM∥DN,再根据平行线的性质可得∠KNM=∠1,由折叠可得∠KMN=∠1,进而得到∠KNM=∠KMN,根据等角对等边可得KN=KM,得到△MNK是等腰三角形;
②利用将矩形纸片沿对角线AC对折,此时折痕为AC,即可得出△MNK是钝角三角形;
③根据当KN=AD=3时,△MNK最小面积求出即可;
④此题要分两种情况进行讨论:①将矩形纸片对折,使点B与点D重合,此时点K也与点D重合;②将矩形纸片沿对角线AC对折,此时折痕为AC,分别进行计算即可.
②利用将矩形纸片沿对角线AC对折,此时折痕为AC,即可得出△MNK是钝角三角形;
③根据当KN=AD=3时,△MNK最小面积求出即可;
④此题要分两种情况进行讨论:①将矩形纸片对折,使点B与点D重合,此时点K也与点D重合;②将矩形纸片沿对角线AC对折,此时折痕为AC,分别进行计算即可.
解答:解: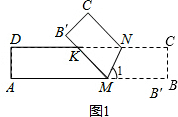 ①如图1,∵四边形ABCD是矩形,
①如图1,∵四边形ABCD是矩形,
∴AM∥DN,
∴∠KNM=∠1.
∵∠KMN=∠1,
∴∠KNM=∠KMN.
∴KN=KM,
∴△MNK是等腰三角形,故此选项正确;
②如图3,△MNK可是钝角三角形,故此选项正确;
③如图1,当KN=AD=3时,此时,△MNK面积最小,△MNK最小面积为:
×3×3=4.5,故此选项正确;
④分两种情况: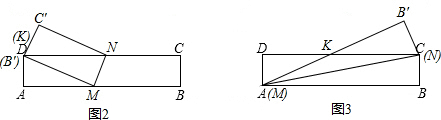
情况一:如图2,将矩形纸片对折,使点B与点D重合,此时点K也与点D重合.
设MK=MD=x,则AM=9-x,
在Rt△DAM中,由勾股定理,得x2=(9-x)2+32,
解得,x=5.
即MD=ND=5,
故S△MNK=S梯形AMND-S△ADM=9×3×
-4×3×
=7.5.
情况二:如图3,将矩形纸片沿对角线AC对折,此时折痕为AC.
设MK=AK=CK=x,则DK=9-x,
同理可得x2=(9-x)2+32,
解得:x=5,
即MK=NK=5.
故S△MNK=S△DAC-S△DAK=
×9×3-
×4×3=7.5,故此选项正确;
故答案为:①②③④.
 ①如图1,∵四边形ABCD是矩形,
①如图1,∵四边形ABCD是矩形,∴AM∥DN,
∴∠KNM=∠1.
∵∠KMN=∠1,
∴∠KNM=∠KMN.
∴KN=KM,
∴△MNK是等腰三角形,故此选项正确;
②如图3,△MNK可是钝角三角形,故此选项正确;
③如图1,当KN=AD=3时,此时,△MNK面积最小,△MNK最小面积为:
| 1 |
| 2 |
④分两种情况:

情况一:如图2,将矩形纸片对折,使点B与点D重合,此时点K也与点D重合.
设MK=MD=x,则AM=9-x,
在Rt△DAM中,由勾股定理,得x2=(9-x)2+32,
解得,x=5.
即MD=ND=5,
故S△MNK=S梯形AMND-S△ADM=9×3×
| 1 |
| 2 |
| 1 |
| 2 |
情况二:如图3,将矩形纸片沿对角线AC对折,此时折痕为AC.
设MK=AK=CK=x,则DK=9-x,
同理可得x2=(9-x)2+32,
解得:x=5,
即MK=NK=5.
故S△MNK=S△DAC-S△DAK=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:①②③④.
点评:此题主要考查了翻折变换、矩形的性质、勾股定理、三角形的面积计算等知识,注意分类思想的运用,综合性较强,有一点的难度.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
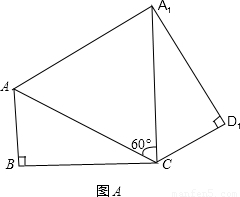
 如图,矩形纸片ABCD中,AB=4,BC=4
如图,矩形纸片ABCD中,AB=4,BC=4
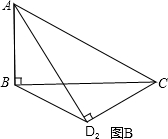

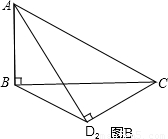
 把△ABC、△ADC沿对角线AC翻折交AD、BC于点F、E.
把△ABC、△ADC沿对角线AC翻折交AD、BC于点F、E. ,将矩形沿对角线AC剪开,解答以下问题:
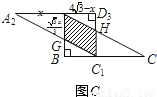
,将矩形沿对角线AC剪开,解答以下问题: ),△A2C1D3是平移后的新位置(图C),若△ABC与△A2C1D3重叠部分的面积为y,求y关于x的函数关系式.
),△A2C1D3是平移后的新位置(图C),若△ABC与△A2C1D3重叠部分的面积为y,求y关于x的函数关系式.



 ,将矩形沿对角线AC剪开,解答以下问题:
,将矩形沿对角线AC剪开,解答以下问题: ),△A2C1D3是平移后的新位置(图C),若△ABC与△A2C1D3重叠部分的面积为y,求y关于x的函数关系式.
),△A2C1D3是平移后的新位置(图C),若△ABC与△A2C1D3重叠部分的面积为y,求y关于x的函数关系式.



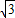 ,将矩形沿对角线AC剪开,解答以下问题:
,将矩形沿对角线AC剪开,解答以下问题: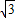 ),△A2C1D3是平移后的新位置(图C),若△ABC与△A2C1D3重叠部分的面积为y,求y关于x的函数关系式.
),△A2C1D3是平移后的新位置(图C),若△ABC与△A2C1D3重叠部分的面积为y,求y关于x的函数关系式.