题目内容
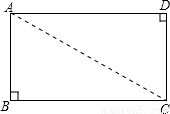
如图,矩形纸片ABCD中,AB=4,BC=4 ,将矩形沿对角线AC剪开,解答以下问题:
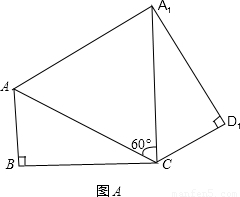
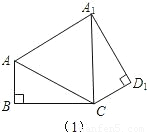
,将矩形沿对角线AC剪开,解答以下问题:(1)在△ACD绕点C顺时针旋转60°,△A1CD1是旋转后的新位置(图A),求此AA1的距离;
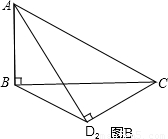
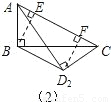
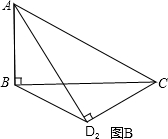
(2)将△ACD沿对角线AC向下翻折(点A、点C位置不动,△ACD和△ABC落在同一平面内),△ACD2是翻折后的新位置(图B),求此时BD2的距离;
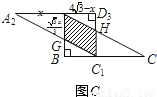
(3)将△ACD沿CB向左平移,设平移的距离为x(0≤x≤4
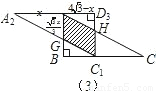
 ),△A2C1D3是平移后的新位置(图C),若△ABC与△A2C1D3重叠部分的面积为y,求y关于x的函数关系式.
),△A2C1D3是平移后的新位置(图C),若△ABC与△A2C1D3重叠部分的面积为y,求y关于x的函数关系式.



【答案】分析:(1)由勾股定理可得AC长度,由于AC=A1C,因为∠ACA1=60°,所以△ACA1为等边三角形,那么AA1=AC
(2)易得BD2是等腰梯形的上底,那么可过梯形上底两个端点作下底的垂线,得到两个全等的直角三角形,把所求线段转移到下底求解.
(3)易得阴影部分为平行四边形,那么可根据相应的三角函数求得阴影部分的底与高.
解答:解:(1)在Rt△ABC中,由勾股定理得,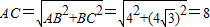 ,
,
在△ACA1中,∵AC=A1C,∠ACA1=60°,
∴△ACA1为等边三角形.
∴AA1=AC=8.(4分)
(2)如图2所示,过B,D2分别作BE⊥AC于E,D2F⊥AC于F,则BE∥D2F,
在Rt△ABC中,∵AB=4,BC=4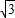 ,tan∠BAC=
,tan∠BAC=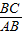 =
=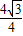 =
= ,
,
∴∠BAC=60°.
在Rt△ABE中,AB=4,∠BAE=60°,∠ABE=30°,
∴AE= AB=2,BE=2
AB=2,BE=2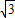 .
.
同理,CF=2,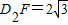 ,
,
∴EF=AC-AE-CF=8-2-2=4,
∵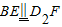 ,
,
∴四边形BEFD2是平行四边形,
∴BD2=EF=4.(8分)
(3)如图3所示,AA2=x,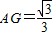 x,
x,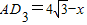 ,
,
∵平移的概念及矩形的性质得AG∥C1H,GC1∥AH,
∴四边形AGC1H是平行四边形,
∴y=S平行四边形AGC1H=AG•AD3=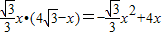 (0≤x≤4
(0≤x≤4 ).(12分)
).(12分)
点评:旋转前后,翻折前后得到的对应线段和角都相等,作等腰梯形的两高构造直角三角形是常用的辅助线方法.
(2)易得BD2是等腰梯形的上底,那么可过梯形上底两个端点作下底的垂线,得到两个全等的直角三角形,把所求线段转移到下底求解.
(3)易得阴影部分为平行四边形,那么可根据相应的三角函数求得阴影部分的底与高.
解答:解:(1)在Rt△ABC中,由勾股定理得,
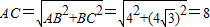 ,
,在△ACA1中,∵AC=A1C,∠ACA1=60°,
∴△ACA1为等边三角形.
∴AA1=AC=8.(4分)
(2)如图2所示,过B,D2分别作BE⊥AC于E,D2F⊥AC于F,则BE∥D2F,
在Rt△ABC中,∵AB=4,BC=4
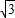 ,tan∠BAC=
,tan∠BAC=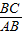 =
=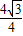 =
= ,
,∴∠BAC=60°.
在Rt△ABE中,AB=4,∠BAE=60°,∠ABE=30°,
∴AE=
 AB=2,BE=2
AB=2,BE=2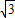 .
.同理,CF=2,
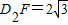 ,
,∴EF=AC-AE-CF=8-2-2=4,
∵
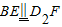 ,
,∴四边形BEFD2是平行四边形,
∴BD2=EF=4.(8分)
(3)如图3所示,AA2=x,
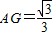 x,
x,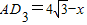 ,
,∵平移的概念及矩形的性质得AG∥C1H,GC1∥AH,
∴四边形AGC1H是平行四边形,
∴y=S平行四边形AGC1H=AG•AD3=
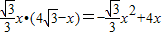 (0≤x≤4
(0≤x≤4 ).(12分)
).(12分)


点评:旋转前后,翻折前后得到的对应线段和角都相等,作等腰梯形的两高构造直角三角形是常用的辅助线方法.

练习册系列答案
相关题目
 如图,矩形纸片ABCD中,AB=4,BC=4
如图,矩形纸片ABCD中,AB=4,BC=4

 把△ABC、△ADC沿对角线AC翻折交AD、BC于点F、E.
把△ABC、△ADC沿对角线AC翻折交AD、BC于点F、E. ,将矩形沿对角线AC剪开,解答以下问题:
,将矩形沿对角线AC剪开,解答以下问题: ),△A2C1D3是平移后的新位置(图C),若△ABC与△A2C1D3重叠部分的面积为y,求y关于x的函数关系式.
),△A2C1D3是平移后的新位置(图C),若△ABC与△A2C1D3重叠部分的面积为y,求y关于x的函数关系式.



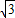 ,将矩形沿对角线AC剪开,解答以下问题:
,将矩形沿对角线AC剪开,解答以下问题: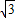 ),△A2C1D3是平移后的新位置(图C),若△ABC与△A2C1D3重叠部分的面积为y,求y关于x的函数关系式.
),△A2C1D3是平移后的新位置(图C),若△ABC与△A2C1D3重叠部分的面积为y,求y关于x的函数关系式.