��Ŀ����
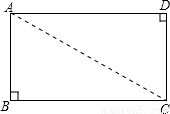
 ��ͼ������ֽƬABCD�У�AB=4��BC=4
��ͼ������ֽƬABCD�У�AB=4��BC=4| 3 |
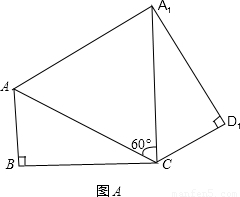
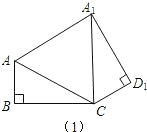
��1���ڡ�ACD�Ƶ�C˳ʱ����ת60�㣬��A1CD1����ת�����λ�ã�ͼA�������AA1�ľ��룻
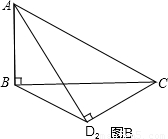
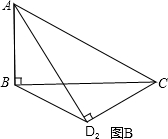
��2������ACD�ضԽ���AC���·��ۣ���A����Cλ�ò�������ACD�͡�ABC����ͬһƽ���ڣ�����ACD2�Ƿ��ۺ����λ�ã�ͼB�������ʱBD2�ľ��룻
��3������ACD��CB����ƽ�ƣ���ƽ�Ƶľ���Ϊx��0��x��4
| 3 |


��������1���ɹ��ɶ����ɵ�AC���ȣ�����AC=A1C����Ϊ��ACA1=60�㣬���ԡ�ACA1Ϊ�ȱ������Σ���ôAA1=AC
��2����BD2�ǵ������ε��ϵף���ô�ɹ������ϵ������˵����µĴ��ߣ��õ�����ȫ�ȵ�ֱ�������Σ��������߶�ת�Ƶ��µ���⣮
��3������Ӱ����Ϊƽ���ı��Σ���ô�ɸ�����Ӧ�����Ǻ��������Ӱ���ֵĵ���ߣ�
��2����BD2�ǵ������ε��ϵף���ô�ɹ������ϵ������˵����µĴ��ߣ��õ�����ȫ�ȵ�ֱ�������Σ��������߶�ת�Ƶ��µ���⣮
��3������Ӱ����Ϊƽ���ı��Σ���ô�ɸ�����Ӧ�����Ǻ��������Ӱ���ֵĵ���ߣ�
����⣺��1����Rt��ABC�У��ɹ��ɶ����ã�AC=
=
=8��
�ڡ�ACA1�У���AC=A1C����ACA1=60�㣬
���ACA1Ϊ�ȱ������Σ�
��AA1=AC=8����4�֣�
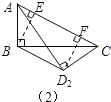
��2����ͼ2��ʾ����B��D2�ֱ���BE��AC��E��D2F��AC��F����BE��D2F��
��Rt��ABC����AB=4��BC=4
��tan��BAC=
=
=
��
���BAC=60�㣮
��Rt��ABE�У�AB=4����BAE=60�㣬��ABE=30�㣬
��AE=
AB=2��BE=2
��
ͬ����CF=2��D2F=2
��
��EF=AC-AE-CF=8-2-2=4��
��BE
D2F��
���ı���BEFD2��ƽ���ı��Σ�
��BD2=EF=4����8�֣�
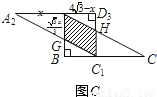
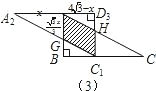
��3����ͼ3��ʾ��AA2=x��AG=
x��AD3=4
-x��
��ƽ�Ƶĸ�����ε����ʵ�AG��C1H��GC1��AH��
���ı���AGC1H��ƽ���ı��Σ�
��y=Sƽ���ı���AGC1H=AG•AD3=
x•(4
-x)=-
x2+4x��0��x��4
������12�֣�
| AB2+BC2 |
42+(4
|
�ڡ�ACA1�У���AC=A1C����ACA1=60�㣬
���ACA1Ϊ�ȱ������Σ�
��AA1=AC=8����4�֣�
��2����ͼ2��ʾ����B��D2�ֱ���BE��AC��E��D2F��AC��F����BE��D2F��
��Rt��ABC����AB=4��BC=4
| 3 |
| BC |
| AB |
4
| ||
| 4 |
| 3 |
���BAC=60�㣮
��Rt��ABE�У�AB=4����BAE=60�㣬��ABE=30�㣬
��AE=
| 1 |
| 2 |
| 3 |
ͬ����CF=2��D2F=2
| 3 |
��EF=AC-AE-CF=8-2-2=4��
��BE
| ||
. |
���ı���BEFD2��ƽ���ı��Σ�
��BD2=EF=4����8�֣�
��3����ͼ3��ʾ��AA2=x��AG=
| ||
| 3 |
| 3 |
��ƽ�Ƶĸ�����ε����ʵ�AG��C1H��GC1��AH��
���ı���AGC1H��ƽ���ı��Σ�
��y=Sƽ���ı���AGC1H=AG•AD3=
| ||
| 3 |
| 3 |
| ||
| 3 |
| 3 |



��������תǰ����ǰ��õ��Ķ�Ӧ�߶κͽǶ���ȣ����������ε����߹���ֱ���������dz��õĸ����߷�����

��ϰ��ϵ�д�
�����Ŀ
 �ѡ�ABC����ADC�ضԽ���AC���۽�AD��BC�ڵ�F��E��
�ѡ�ABC����ADC�ضԽ���AC���۽�AD��BC�ڵ�F��E�� ���������ضԽ���AC����������������⣺
���������ضԽ���AC����������������⣺ ������A2C1D3��ƽ�ƺ����λ�ã�ͼC��������ABC���A2C1D3�ص����ֵ����Ϊy����y����x�ĺ�����ϵʽ��
������A2C1D3��ƽ�ƺ����λ�ã�ͼC��������ABC���A2C1D3�ص����ֵ����Ϊy����y����x�ĺ�����ϵʽ��



 ���������ضԽ���AC����������������⣺
���������ضԽ���AC����������������⣺ ������A2C1D3��ƽ�ƺ����λ�ã�ͼC��������ABC���A2C1D3�ص����ֵ����Ϊy����y����x�ĺ�����ϵʽ��
������A2C1D3��ƽ�ƺ����λ�ã�ͼC��������ABC���A2C1D3�ص����ֵ����Ϊy����y����x�ĺ�����ϵʽ��



 ���������ضԽ���AC����������������⣺
���������ضԽ���AC����������������⣺ ������A2C1D3��ƽ�ƺ����λ�ã�ͼC��������ABC���A2C1D3�ص����ֵ����Ϊy����y����x�ĺ�����ϵʽ��
������A2C1D3��ƽ�ƺ����λ�ã�ͼC��������ABC���A2C1D3�ص����ֵ����Ϊy����y����x�ĺ�����ϵʽ��