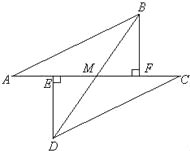
题目内容
【题目】(1)如图 1,在四边形 ABCD 中,AB∥DC,E 是 BC 中点,若 AE 是∠BAD 的平分线,试探究 AB,AD,DC 之间的数量关系,请直接写出结论,无需证明.
(2)如图 2,在四边形ABCD 中,AB∥DC,AF 与DC 的延长线交于点F,E 是BC 中点,若AE 是∠BAF 的平分线,试探究AB,AF,CF 之间的数量关系,证明你的结论.

【答案】(1)AD=AB+DC;(2)AB=AF+CF,证明详见解析.
【解析】
(1)延长AE交DC的延长线于点F,证明△AEB≌△FEC,根据全等三角形的性质得到AB=FC,根据等腰三角形的判定得到DF=AD,证明结论;
(2)延长AE交DF的延长线于点G,利用同(1)相同的方法证明.
(1)延长AE交DC的延长线于点F.
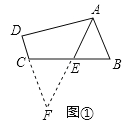
∵E是BC的中点,∴CE=BE.
∵AB∥DC,∴∠BAE=∠F.
在△AEB和△FEC中,∵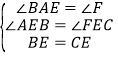 ,∴△AEB≌△FEC,∴AB=FC.
,∴△AEB≌△FEC,∴AB=FC.
∵AE是∠BAD的平分线,∴∠BAE=∠EAD.
∵∠BAE=∠F,∴∠EAD=∠F,∴AD=DF,∴AD=DF=DC+CF=DC+AB;
(2)如图②,延长AE交DF的延长线于点G.
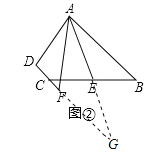
∵E是BC的中点,∴CE=BE.
∵AB∥DC,∴∠BAE=∠G.
在△AEB和△GEC中,∵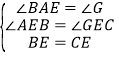 ,∴△AEB≌△GEC,∴AB=GC.
,∴△AEB≌△GEC,∴AB=GC.
∵AE是∠BAF的平分线,∴∠BAG=∠FAG.
∵∠BAE=∠G,∴∠FAG=∠G,∴FA=FG,∴AB=CG=AF+CF.

练习册系列答案
相关题目