题目内容
【题目】一辆慢车从甲地匀速行驶至乙地，一辆快车同时从乙地出发匀速行驶至甲地，两车之间的距离y（千米）与行驶时间x（小时）的对应关系如图所示：
（1）甲乙两地相距 千米，慢车速度为 千米/小时．
（2）求快车速度是多少？
（3）求从两车相遇到快车到达甲地时y与x之间的函数关系式．
（4）直接写出两车相距300千米时的x值．
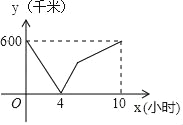
【答案】（1）600， 60；（2）快车速度是90千米/小时；（3）从两车相遇到快车到达甲地时y与x之间的函数关系式为y=150x﹣600；（4）当x=2小时或x=6小时时，两车相距300千米．
【解析】
1）由当x=0时y=600可得出甲乙两地间距，再利用速度=两地间距÷慢车行驶的时间，即可求出慢车的速度；
（2）设快车的速度为a千米/小时，根据两地间距=两车速度之和×相遇时间，即可得出关于a的一元一次方程，解之即可得出结论；
（3）分别求出快车到达甲地的时间及快车到达甲地时两车之间的间距，根据函数图象上点的坐标，利用待定系数法即可求出该函数关系式；
（4）利用待定系数法求出当0≤x≤4时y与x之间的函数关系式，将y=300分别代入0≤x≤4时及4≤x≤
时的函数关系式中求出x值，此题得解．
（1）∵当x=0时，y=600，
∴甲乙两地相距600千米．
600÷10=60（千米/小时）．
故答案为：600；60．
（2）设快车的速度为a千米/小时，
根据题意得：4（60+a）=600，
解得：a=90．
答：快车速度是90千米/小时．
（3）快车到达甲地的时间为600÷90=（小时），
当x=时，两车之间的距离为60×=400（千米）．
设当4≤x≤时，y与x之间的函数关系式为y=kx+b（k≠0），
∵该函数图象经过点（4，0）和（，400），
∴
，解得：
，
∴从两车相遇到快车到达甲地时y与x之间的函数关系式为y=150x﹣600．
（4）设当0≤x≤4时，y与x之间的函数关系式为y=mx+n（m≠0），
∵该函数图象经过点（0，600）和（4，0），
∴
，解得：
，
∴y与x之间的函数关系式为y=﹣150x+600．
当y=300时，有﹣150x+600=300或150x﹣600=300，
解得：x=2或x=6．
∴当x=2小时或x=6小时时，两车相距300千米．
