题目内容
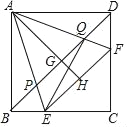
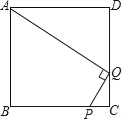
【题目】如图,Q为正方形ABCD的CD边上一点,CQ=1,DQ=2,P为BC上一点,若PQ⊥AQ,则CP=_____.
【答案】![]()
【解析】
证明△ADQ∽△QCP:已知的条件有∠C=∠D=90°,那么只要得出另外两组对应角相等即可得出两三角形相似,因为∠DQA+∠CQP=180°-90°=90°,而∠DAQ+∠DQA=90°,因此∠CQP=∠DAQ,那么就构成了两三角形相似的条件;然后由相似三角形的对应边成比例、正方形的四条边都相等及已知条件CQ=1,DQ=2求解即可.
解:∵PQ⊥AQ,
∴∠DQA+∠CQP=180°-90°=90°;
又∵四边形ABCD是正方形,
∴∠DAQ+∠DQA=90°,
∴∠CQP=∠DAQ,
∴ADQ∽△QCP,
![]() ,
,
∵CQ=1,DQ=2,
∴AD=DC=3;
∴CP=![]() ,
,
故答案为:![]() .
.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目