题目内容
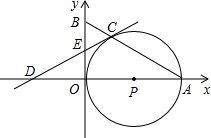 如图,点A在x轴的正半轴上,以OA为直径作⊙P,C是⊙P上一点,过点C的直线y=
如图,点A在x轴的正半轴上,以OA为直径作⊙P,C是⊙P上一点,过点C的直线y=
| ||
| 3 |
| 3 |
| 3 |
(1)求证:OE=CE;
(2)请判断直线CD与⊙P位置关系,证明你的结论,并请求出⊙P的半径长.
分析:(1)连接OC,利用已知条件计算出CE和OB的长度,再证明△BCO为直角三角形,利用:直角三角形斜边上的中线等于斜边的一半即可证明OE=CE;
(2)①直线CD是⊙P的切线,证明PC⊥CD.②设⊙P的半径为r,则在Rt△PCD中,由勾股定理得到关于r的方程,求出r即可.
(2)①直线CD是⊙P的切线,证明PC⊥CD.②设⊙P的半径为r,则在Rt△PCD中,由勾股定理得到关于r的方程,求出r即可.
解答:解:(1)证明:连接OC,
∵直线y=
x+2
与y轴相交于点E,
∴点E的坐标为(0,2
),即OE=2
.
又∵点B的坐标为(0,4
),
∴OB=4
,
∴BE=OE=2
,
又∵OA是⊙P的直径,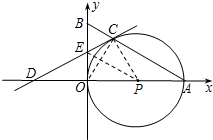
∴∠ACO=90°,即OC⊥AB,
∴OE=CE(直角三角形斜边上的中线等于斜边的一半)
(2)直线CD是⊙P的切线.
①证明:连接PC、PE,由①可知:OE=CE.
在△POE和△PCE,
,
∴△POE≌△PCE,
∴∠POE=∠PCE.
又∵x轴⊥y轴,
∴∠POE=∠PCE=90°,
∴PC⊥CE,即:PC⊥CD.
又∵直线CD经过半径PC的外端点C,
∴直线CD是⊙P的切线;
②∵对y=
x+2
,当y=0时,x=-6,即OD=6,
在Rt△DOE中,DE=
=
=4
,
∴CD=DE+EC=DE+OE=4
+2
=6
.
设⊙P的半径为r,则在Rt△PCD中,由勾股定理知PC2+CD2=PD2,
即 r2+(6
)2=(6+r)2,
解得 r=6,即⊙P的半径长为6.
∵直线y=
| ||
| 3 |
| 3 |
∴点E的坐标为(0,2
| 3 |
| 3 |
又∵点B的坐标为(0,4
| 3 |
∴OB=4
| 3 |
∴BE=OE=2
| 3 |
又∵OA是⊙P的直径,

∴∠ACO=90°,即OC⊥AB,
∴OE=CE(直角三角形斜边上的中线等于斜边的一半)
(2)直线CD是⊙P的切线.
①证明:连接PC、PE,由①可知:OE=CE.
在△POE和△PCE,
|
∴△POE≌△PCE,
∴∠POE=∠PCE.
又∵x轴⊥y轴,
∴∠POE=∠PCE=90°,
∴PC⊥CE,即:PC⊥CD.
又∵直线CD经过半径PC的外端点C,
∴直线CD是⊙P的切线;
②∵对y=
| ||
| 3 |
| 3 |
在Rt△DOE中,DE=
| OD2+OE2 |
62+(2
|
| 3 |
∴CD=DE+EC=DE+OE=4
| 3 |
| 3 |
| 3 |
设⊙P的半径为r,则在Rt△PCD中,由勾股定理知PC2+CD2=PD2,
即 r2+(6
| 3 |
解得 r=6,即⊙P的半径长为6.
点评:本题综合考查了切线的性质、判定定理、勾股定理以及直角三角形的性质:直角三角形斜边上的中线等于斜边的一半,具有较强的综合性,有一定的难度.

练习册系列答案
相关题目
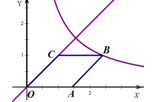
 (2013•金华模拟)如图,点A在x轴的正半轴,菱形OABC的面积为
(2013•金华模拟)如图,点A在x轴的正半轴,菱形OABC的面积为 如图,点P在y轴的正半轴上,⊙P交x轴于B、C两点,以AC为直角边作等腰Rt△ACD,BD分别交y轴和⊙P于E、F两点,交连接AC、FC.
如图,点P在y轴的正半轴上,⊙P交x轴于B、C两点,以AC为直角边作等腰Rt△ACD,BD分别交y轴和⊙P于E、F两点,交连接AC、FC. ,点B在双曲线
,点B在双曲线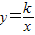 上,点C在直线y=x上,则k的值为 .
上,点C在直线y=x上,则k的值为 .
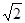 ,点B在双曲线
,点B在双曲线 上,点C在直线y=x上,则k的值为____________.
上,点C在直线y=x上,则k的值为____________.