题目内容
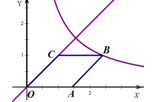
如图,点A在x轴的正半轴,菱形OABC的面积为 ,点B在双曲线
,点B在双曲线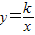 上,点C在直线y=x上,则k的值为 .
上,点C在直线y=x上,则k的值为 .
【答案】分析:首先根据直线y=x经过点C,设C点坐标为(a,a),再利用勾股定理算出CO=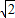 a,进而得到AO=CO=CB=AB=
a,进而得到AO=CO=CB=AB= a,再利用菱形的面积公式计算出a的值,进而得到C点坐标,进而得到B点坐标,即可求出k的值.
a,再利用菱形的面积公式计算出a的值,进而得到C点坐标,进而得到B点坐标,即可求出k的值.
解答:解:∵直线y=x经过点C,
∴设C(a,a),
∴OC2=2a2,
∴CO= a,
a,
∵四边形OABC是菱形,
∴AO=CO=CB=AB=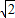 a,
a,
∵菱形OABC的面积是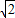 ,
,
∴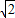 a•a=
a•a= ,
,
∴a=1,
∴CB=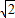 ,C(1,1)
,C(1,1)
∴B(1+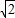 ,1),
,1),
设反比例函数解析式为y=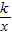 (k≠0),
(k≠0),
∵B(1+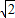 ,1)在反比例函数图象上,
,1)在反比例函数图象上,
∴k=(1+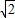 )×1=
)×1=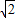 +1,
+1,
故答案为: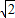 +1.
+1.
点评:此题主要考查了待定系数法求反比例函数,菱形的面积公式,菱形的性质,关键是根据菱形的面积求出C点坐标,进而得到B点坐标,即可算出反比例函数解析式.
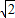 a,进而得到AO=CO=CB=AB=
a,进而得到AO=CO=CB=AB= a,再利用菱形的面积公式计算出a的值,进而得到C点坐标,进而得到B点坐标,即可求出k的值.
a,再利用菱形的面积公式计算出a的值,进而得到C点坐标,进而得到B点坐标,即可求出k的值.解答:解:∵直线y=x经过点C,
∴设C(a,a),
∴OC2=2a2,
∴CO=
 a,
a,∵四边形OABC是菱形,
∴AO=CO=CB=AB=
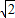 a,
a,∵菱形OABC的面积是
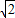 ,
,∴
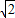 a•a=
a•a= ,
,∴a=1,
∴CB=
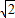 ,C(1,1)
,C(1,1)∴B(1+
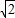 ,1),
,1),设反比例函数解析式为y=
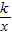 (k≠0),
(k≠0),∵B(1+
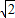 ,1)在反比例函数图象上,
,1)在反比例函数图象上,∴k=(1+
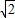 )×1=
)×1=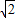 +1,
+1,故答案为:
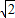 +1.
+1.点评:此题主要考查了待定系数法求反比例函数,菱形的面积公式,菱形的性质,关键是根据菱形的面积求出C点坐标,进而得到B点坐标,即可算出反比例函数解析式.

练习册系列答案
相关题目
 (2013•金华模拟)如图,点A在x轴的正半轴,菱形OABC的面积为
(2013•金华模拟)如图,点A在x轴的正半轴,菱形OABC的面积为 如图,点P在y轴的正半轴上,⊙P交x轴于B、C两点,以AC为直角边作等腰Rt△ACD,BD分别交y轴和⊙P于E、F两点,交连接AC、FC.
如图,点P在y轴的正半轴上,⊙P交x轴于B、C两点,以AC为直角边作等腰Rt△ACD,BD分别交y轴和⊙P于E、F两点,交连接AC、FC. 如图,点A在x轴的正半轴上,以OA为直径作⊙P,C是⊙P上一点,过点C的直线
如图,点A在x轴的正半轴上,以OA为直径作⊙P,C是⊙P上一点,过点C的直线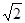 ,点B在双曲线
,点B在双曲线 上,点C在直线y=x上,则k的值为____________.
上,点C在直线y=x上,则k的值为____________.