题目内容
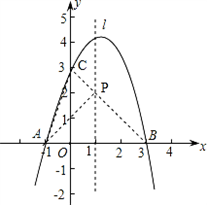
已知抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴.
(1)求抛物线的函数关系式;
(2)设点P是直线l上的一个动点,当△PAC的周长最小时,求点P的坐标;
(3)在直线l上是否存在点M,使△MAC为等腰三角形?若存在,直接写出所有符合条件的点M的坐标;若不存在,请说明理由.
(1)求抛物线的函数关系式;
(2)设点P是直线l上的一个动点,当△PAC的周长最小时,求点P的坐标;
(3)在直线l上是否存在点M,使△MAC为等腰三角形?若存在,直接写出所有符合条件的点M的坐标;若不存在,请说明理由.
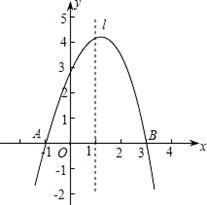
| 解:(1)将A(﹣1,0)、B(3,0)、C(0,3) 代入抛物线y=ax2+bx+c中, 得: 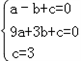 ,解得: ,解得: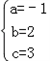 ∴抛物线的解析式:y=﹣x2+2x+3; (2)连接BC,直线BC与直线l的交点为P; 设直线BC的解析式为y=kx+b, 将B(3,0),C(0,3)代入上式, 得: 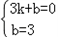 ,解得: ,解得: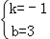 ∴直线BC的函数关系式y=﹣x+3; 当x=1时,y=2,即P的坐标(1,2); (3)抛物线的解析式为:x=﹣ 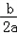 =1, =1,设M(1,m),已知A(﹣1,0)、C(0,3), 则:MA2=m2+4,MC2=m2﹣6m+10,AC2=10; ①若MA=MC,则MA2=MC2, 得:m2+4=m2﹣6m+10, 得:m=1; ②若MA=AC,则MA2=AC2, 得:m2+4=10,得:m=± 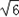 ; ;③若MC=AC,则MC2=AC2, 得:m2﹣6m+10=10, 得:m=0,m=6; 当m=6时,M、A、C三点共线,构不成三角形, 不合题意,故舍去; 综上可知,符合条件的M点存在, 且坐标为 M(1, 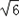 )(1,﹣ )(1,﹣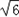 )(1,1)(1,0). )(1,1)(1,0). |
 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
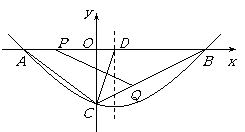 (3)在(2)的结论下,直线x=1上是否存在点M,使△MPQ为等腰三角形?若存在,请求出所有点M的坐
(3)在(2)的结论下,直线x=1上是否存在点M,使△MPQ为等腰三角形?若存在,请求出所有点M的坐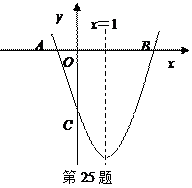 (3)设点P为抛物线的对称轴x=1上的一动点,求使∠PCB=90°的点P的坐标.
(3)设点P为抛物线的对称轴x=1上的一动点,求使∠PCB=90°的点P的坐标.

 轴,交直线BC于点F,求线段DF的长,并求△BCD的面积;
轴,交直线BC于点F,求线段DF的长,并求△BCD的面积;