题目内容
已知抛物线y=ax2+bx-4a经过A(-1,0)、C(0,4)两点,与x轴交于另一点B.
(1)求抛物线的解析式;
(2)若点D(m,m+1)在第一象限的抛物线上, 求点D关于直线BC对称的点的坐标;
(3)在(2)的条件下,连结BD,若点P为抛物线上一点,且∠DBP=45°,求点P的坐标.
解:(1)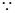 抛物线
抛物线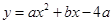 经过
经过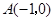 ,
, 两点,
两点,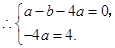
解得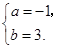
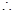 抛物线的解析式为
抛物线的解析式为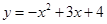 .
.
(2) 点
点 在抛物线上,
在抛物线上,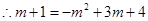 .
.
∴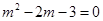 .
.  或
或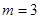 .
.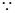 点D在第一象限,
点D在第一象限, 舍去.
舍去. 点D的坐标为
点D的坐标为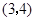 .
. 抛物线
抛物线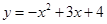 与
与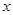 轴的另一交点
轴的另一交点 的坐标为
的坐标为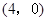 ,
, ,
,
∴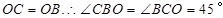 .
.
设点 关于直线
关于直线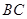 的对称点为点
的对称点为点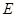 .
.
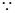
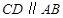 ,
, 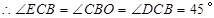 .
.
∴E点在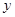 轴上,且
轴上,且 .
.
∴OE=1.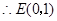 .
.
即点 关于直线
关于直线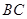 对称的点的坐标为(0,1).
对称的点的坐标为(0,1).
(3)过点 作
作 的垂线交直线
的垂线交直线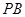 于点
于点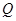 ,过点
,过点 作
作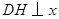 轴于
轴于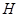 ,过点
,过点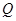 作
作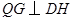 于
于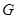 .
.
∴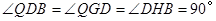 ..
..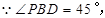
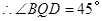 .
.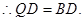
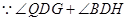
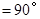 ,
,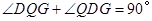 ,
,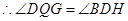 .
.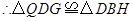 .
. 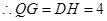 ,
,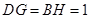 .
.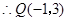 .
.
设直线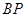 的解析式为
的解析式为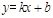 .
.
由点 ,点
,点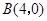 ,求得直线
,求得直线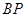 的解析式为
的解析式为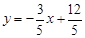 .
.
解方程组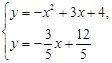
得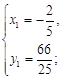
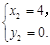 (舍)
(舍)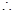 点
点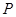 的坐标为
的坐标为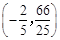 .
.
解析

练习册系列答案
相关题目
 (3)在(2)的结论下,直线x=1上是否存在点M,使△MPQ为等腰三角形?若存在,请求出所有点M的坐
(3)在(2)的结论下,直线x=1上是否存在点M,使△MPQ为等腰三角形?若存在,请求出所有点M的坐 (3)设点P为抛物线的对称轴x=1上的一动点,求使∠PCB=90°的点P的坐标.
(3)设点P为抛物线的对称轴x=1上的一动点,求使∠PCB=90°的点P的坐标.
 轴,交直线BC于点F,求线段DF的长,并求△BCD的面积;
轴,交直线BC于点F,求线段DF的长,并求△BCD的面积;