题目内容
【题目】在四边形ABDC中，AC＝AB，DC＝DB，∠CAB＝60°，∠CDB＝120°，E是AC上一点，F是AB延长线上一点，且CE＝BF．
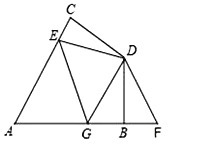
（1）试说明：DE＝DF；
（2）在图中，若G在AB上且∠EDG＝60°，试猜想CE、EG、BG之间的数量关系并证明所归纳结论；
（3）若题中条件“∠CAB＝60°，∠CDB＝120°”改为∠CAB＝α，∠CDB＝180°－α，G在AB上，∠EDG满足什么条件时，(2)中结论仍然成立？（只写结果不要证明）．
【答案】（1）证明见解析；
（2）CE、EG、BG之间的数量关系为：CE+BG=EG，证明见解析；
（3）当∠EDG=90°﹣
α时， CE+BG=EG仍然成立．
【解析】试题分析：（1）首先判断出∠C=∠DBF，然后根据全等三角形判定的方法，判断出△CDE≌△BDF，即可判断出DE=DF．（2）猜想CE、EG、BG之间的数量关系为：CE+BG=EG．首先根据全等三角形判定的方法，判断出△ABD≌△ACD，即可判断出∠BDA=∠CDA=60°；然后根据∠EDG=60°，可得∠CDE=∠ADG，∠ADE=∠BDG，再根据∠CDE=∠BDF，判断出∠EDG=∠FDG，据此推得△DEG≌△DFG，所以EG=FG，最后根据CE=BF，判断出CE+BG=EG即可．（3）根据（2）的证明过程，要使CE+BG=EG仍然成立，则∠EDG=∠BDA=∠CDA=
∠CDB，即∠EDG=
（180°-α）=90°-
α，据此解答即可．
试题解析：（1）：∵∠CAB+∠C+∠CDB+∠ABD=360°，∠CAB=60°，∠CDB=120°，
∴∠C+∠ABD=360°﹣60°﹣120°=180°，
又∵∠DBF+∠ABD=180°，
∴∠C=∠DBF，
在△CDE和△BDF中，
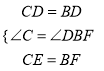（SAS）
∴△CDE≌△BDF，
∴DE=DF．
(2)解：如图1，连接AD，猜想CE、EG、BG之间的数量关系为：CE+BG=EG．
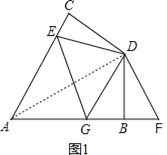
证明：在△ABD和△ACD中，
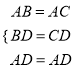（SSS）
∴△ABD≌△ACD，
∴∠BDA=∠CDA=
∠CDB=
×120°=60°，
又∵∠EDG=60°，
∴∠CDE=∠ADG，∠ADE=∠BDG，
由（1），可得△CDE≌△BDF，
∴∠CDE=∠BDF，
∴∠BDG+∠BDF=60°，
即∠FDG=60°，
∴∠EDG=∠FDG，
在△DEG和△DFG中，
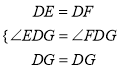
∴△DEG≌△DFG，
∴EG=FG，
又∵CE=BF，FG=BF+BG，
∴CE+BG=EG；
(3)解：要使CE+BG=EG仍然成立，
则∠EDG=∠BDA=∠CDA=
∠CDB，
即∠EDG=
（180°﹣α）=90°﹣
α，
∴当∠EDG=90°﹣
α时， CE+BG=EG仍然成立．
