��Ŀ����
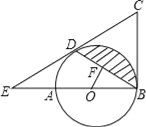
����Ŀ������֪����ͼ�٣���Rt��ABC������C��90�㣬AC��BC����D��E�ֱ��ڱ�AC��BC�ϣ���DE��AB����֤AD��BE������Ҫ֤����.
��̽��������ͼ���е�AE����M��N��P�ֱ�ΪDE��AE��AB���е㣬˳������M��N��P�������������䣬��ͼ������֤����MNP�ǵ���ֱ��������.
��Ӧ�á���ͼ���еĵ�D��E�ֱ��ƶ���AC��BC���ӳ������������������䣬������BD����ȡ���е�Q��˳������M��N��P��Q����ͼ�ۣ���![]() ��
��![]() ����DE��
����DE��![]() �����ı���MNPQ�����Ϊ .
�����ı���MNPQ�����Ϊ .



���𰸡�֤��������
�����������������
(1) Ҫ֤����MNP�ǵ���ֱ�������Σ�����Ҫ֤��MN=PN�Լ���MNP=90��. �ɡ���֪�����ڿ�֪����֤AD=BE����������֪MN��PN�ֱ�Ϊ��AED���BAE����λ�ߣ��ʲ���֤��MN=PN. ͨ����λ�ߵõ���ƽ�й�ϵ������ͬλ�Ǻ��ڴ��ǿɽ���MNPת��ΪRt��ACE�������֮�ͣ�����֤����MNP=90��������֤����MNP�ǵ���ֱ��������.
(2) ���������֪���ı���MNPQ�������߾�Ϊ��Ӧ�����ε���λ��. �ݴ˲���֤���ı���MNPQ��ƽ���ı���. ���ݵ���ֱ��������ABC�������������֤����NPQΪֱ�ǣ�����֤���ı���MNPQ�Ǿ���. ������֪�����������AB�ij����ٸ��ݵ���ֱ��������ABC��������������BC��AC�ij��������������������ο������EC��CD�ij�. �ڴ˻����ϸ�����λ�߶������ѻ��NP��PQ�ij���������þ���MNPQ�����.
���������
(1) ������̽��������.
֤������DE��AB��
��![]() ��
��
��AC=BC��
��AD=BE.
�ߵ�M���N�ֱ�ΪDE��AE���е㣬
��MN��AD�� ![]() ��
��
���MNE=��CAE.
�ߵ�N���P�ֱ�ΪAE��AB���е㣬
��NP��BE�� ![]() ��
��
���PNE=��AEC.
��AD=BE��
��MN=PN.
�ߡ�C=90����
����Rt��ACE����CAE+��AEC=90����
���MNP=��MNE+��PNE=��CAE+��AEC=90��.
��MN=PN����MNP=90����
���MNP�ǵ���ֱ��������.
(2) ������Ӧ�á�����.
��С��Ӧ��д��4. ����������.
�ߵ�M���N�ֱ�ΪDE��AE���е㣬
��MN��AD��
�ߵ�P���Q�ֱ�ΪAB��BD���е㣬
��PQ��AD�� ![]() ��
��
��MN��PQ.
ͬ����NP��BE�� ![]() ��MQ��BE��
��MQ��BE��
��NP��MQ.
��MN��PQ��NP��MQ��
���ı���MNPQΪƽ���ı���.
�ߡ�ACB=90����AC=BC��
���ABC=��BAC=45����
��NP��BE��
���APN=��ABC=45����
��PQ��AD��
���BPQ=��BAC=45����
���NPQ=180��-��APN-��BPQ=180��-45��-45��=90����
��ƽ���ı���MNPQΪ����.
��![]() ��
�� ![]() ��
��
��![]() ��
��
�ߡ�ACB=90������ABC=45����AC=BC��
����Rt��ACB�� ![]() .
.
��AC=BC=3.
��DE��AB��
���ECD�ס�BCA��
��![]() ��
��
��![]() ��
�� ![]() .
.
��BE=BC+EC=3+1=4��AD=AC+CD=3+1=4.
��![]() ��
�� ![]() ��
��
������MNPQ�����Ϊ![]() �����ı���MNPQ�����Ϊ4.
�����ı���MNPQ�����Ϊ4.

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�����Ŀ��ij�̳�������һ����������ת����ת��(��ͼ)�����涨���˿���10Ԫ���Ͼ��ܻ��һ��ת��ת�̵Ļ��ᣬ��ת��ֹͣʱ��ָ��������һ����Ϳ��Ի����Ӧ�Ľ�Ʒ���±��ǻ�����е�һ��ͳ�����ݣ�

(1)���㲢��ɱ���
ת��ת�̵Ĵ���n | 100 | 150 | 200 | 500 | 800 | 1000 |
���ڡ�Ǧ�ʡ��Ĵ���m | 68 | 111 | 136 | 345 | 546 | 701 |
���ڡ�Ǧ�ʡ���Ƶ�� |
(2)������ȥת����ת��һ�Σ�����Ǧ�ʵĸ���Լ�Ƕ��٣�