题目内容
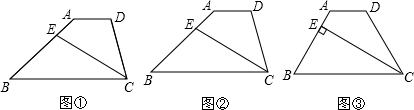
已知:如图,在梯形ABCD中,AD∥BC,BC=3AD.(1)如图①,连接AC,如果三角形ADC的面积为6,求梯形ABCD的面积;
(2)如图②,E是腰AB上一点,连接CE,设△BCE和四边形AECD的面积分别为S1和S2,且2S1=3S2,求
| AE | BE |
(3)如图③,AB=CD,如果CE⊥AB于点E,且BE=3AE,求∠B的度数.
分析:(1)由△ADC与△ABC等高,且BC=3AD,可得△ABC的面积是△ADC面积的三倍,所以可求得△ADC的面积,即可求得梯形ABCD的面积;
(2)可利用面积法求解,因为如果三角形的高相等,则其面积的比等于其底的比,所以可求得AE与BE的比;
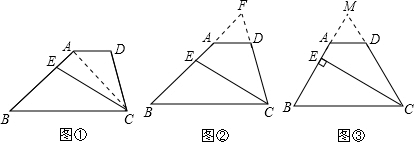
(3)首先延长BA与CD,然后根据面积的关系求得△MBC是等边三角形,即可得∠B为60°.
(2)可利用面积法求解,因为如果三角形的高相等,则其面积的比等于其底的比,所以可求得AE与BE的比;
(3)首先延长BA与CD,然后根据面积的关系求得△MBC是等边三角形,即可得∠B为60°.
解答:解:(1)在梯形ABCD中,
∵AD∥BC,又△ADC与△ABC等高,且BC=3AD,
∴S△ABC=3S△ADC,
∵S△ADC=6,
∴S梯形ABCD=S△ABC+S△ACD=4S△ADC=24.
(2)方法1:连接AC,如图①,设△AEC的面积为S3,则△ACD的面积为S2-S3,
由(1)和已知可得
解得:S1=4S3.
∴
=
.
∵△AEC与△BEC等高,
∴
=
.
方法2:延长BA、CD相交于点F,如图②
∵AD∥BC,
∴△FAD∽△FBC,
∴
=(
)2=
,
设S△FAD=S3=a,则S△FBC=9a,S1+S2=8a,
又∵2S1=3S2,
∴S1=
a,S2=
a,S3=a.
∵△EFC与△CEB等高,
∴
=
=
=
.
设FE=7k,则BE=8k,FB=15k,
∴FA=
FB=5k.
∴AE=7k-5k=2k.
∴
=
.
(3)延长BA、CD相交于点M.如图③,
∵AD∥BC,
∴△MAD∽△MBC,
∴
=
=
.
∴MB=3MA.设MA=2x,则MB=6x.
∴AB=4x.
∵BE=3AE,
∴BE=3x,AE=x.
∴BE=EM=3x,E为MB的中点.
又∵CE⊥AB,
∴CB=MC.
又∵MB=MC,
∴△MBC为等边三角形.
∴∠B=60°.
∵AD∥BC,又△ADC与△ABC等高,且BC=3AD,
∴S△ABC=3S△ADC,
∵S△ADC=6,
∴S梯形ABCD=S△ABC+S△ACD=4S△ADC=24.
(2)方法1:连接AC,如图①,设△AEC的面积为S3,则△ACD的面积为S2-S3,

由(1)和已知可得
|
解得:S1=4S3.
∴
| S3 |
| S1 |
| 1 |
| 4 |
∵△AEC与△BEC等高,
∴
| AE |
| BE |
| 1 |
| 4 |
方法2:延长BA、CD相交于点F,如图②
∵AD∥BC,
∴△FAD∽△FBC,
∴
| S△FAD |
| S△FBC |
| AD |
| BC |
| 1 |
| 9 |
设S△FAD=S3=a,则S△FBC=9a,S1+S2=8a,
又∵2S1=3S2,
∴S1=
| 24 |
| 5 |
| 16 |
| 5 |
∵△EFC与△CEB等高,
∴
| FE |
| EB |
| S△FEC |
| S△ECB |
| S3+S2 |
| S1 |
| 7 |
| 8 |
设FE=7k,则BE=8k,FB=15k,
∴FA=
| 1 |
| 3 |
∴AE=7k-5k=2k.
∴
| AE |
| BE |
| 1 |
| 4 |
(3)延长BA、CD相交于点M.如图③,
∵AD∥BC,
∴△MAD∽△MBC,
∴
| AD |
| BC |
| MA |
| MB |
| 1 |
| 3 |
∴MB=3MA.设MA=2x,则MB=6x.
∴AB=4x.
∵BE=3AE,
∴BE=3x,AE=x.
∴BE=EM=3x,E为MB的中点.
又∵CE⊥AB,
∴CB=MC.
又∵MB=MC,
∴△MBC为等边三角形.
∴∠B=60°.
点评:此题考查了如果三角形的高相等,则面积比等于其底边的比.解此题的关键是准确的作出辅助线与数形结合思想的应用.

练习册系列答案
相关题目
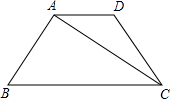 已知:如图,在梯形ABCD中,AD∥BC,AB=DC,∠D=120°,对角线CA平分∠BCD,且梯形的周长为20,求AC的长及梯形面积S.
已知:如图,在梯形ABCD中,AD∥BC,AB=DC,∠D=120°,对角线CA平分∠BCD,且梯形的周长为20,求AC的长及梯形面积S.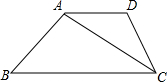 已知:如图,在梯形ABCD中,AD∥BC,∠B=45°,∠BAC=105°,AD=CD=4,
已知:如图,在梯形ABCD中,AD∥BC,∠B=45°,∠BAC=105°,AD=CD=4,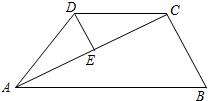 已知:如图,在梯形ABCD中,AB∥CD,AC⊥BC,AC平分∠DAB,点E为AC的中点.求证:DE=
已知:如图,在梯形ABCD中,AB∥CD,AC⊥BC,AC平分∠DAB,点E为AC的中点.求证:DE=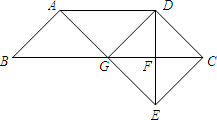 (2013•闵行区二模)已知:如图,在梯形ABCD中,AD∥BC,AB=CD,BC=2AD.DE⊥BC,垂足为点F,且F是DE的中点,联结AE,交边BC于点G.
(2013•闵行区二模)已知:如图,在梯形ABCD中,AD∥BC,AB=CD,BC=2AD.DE⊥BC,垂足为点F,且F是DE的中点,联结AE,交边BC于点G. 已知:如图,在梯形ABCD中,AD∥BC,CD=10cm,∠B=45度,∠C=30度,AD=5cm.
已知:如图,在梯形ABCD中,AD∥BC,CD=10cm,∠B=45度,∠C=30度,AD=5cm.