题目内容
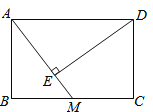
【题目】如图,在矩形ABCD中,AB=2,BC=3,M为BC中点,连接AM,过D作DE⊥AM于E,则DE的长度为_______________.
【答案】![]()
【解析】首先根据矩形的性质,求得AD∥BC,即可得到∠DAE=∠AMB,又由∠DEA=∠B,根据有两角对应相等的三角形相似,可得△DAE∽△AMB,由△ABM∽△ADE可以得到
![]() ,根据勾股定理可以求得AD的长,继而得到答案.
,根据勾股定理可以求得AD的长,继而得到答案.
解:在矩形ABCD中,
∵AD∥BC,
∵M是边BC的中点,BC=3,AB=2,
∵∠DEA=∠B=90°,
∴AM=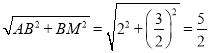 ,
,
∴∠DAE=∠AMB,
∴![]() ,即
,即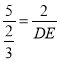 ,
,
∴DE=![]() .
.
故答案为![]() .
.
“点睛”此题考查了相似三角形的判定与性质,以及矩形的性质.解题时要注意识图,准确应用数形结合思想.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目