题目内容
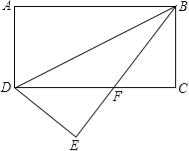
【题目】如图,将矩形ABCD沿BD对折,点A落在E处,BE与CD相交于F,若AD=3,BD=6.
(1)求证:△EDF≌△CBF;
(2)求∠EBC.
【答案】(1)证明见解析
(2)∠EBC=30°.
【解析】试题分析:(1)由矩形的性质和折叠的性质可得DE=BC,∠E=∠C=90°,对顶角∠DFE=∠BFC,利用AAS可判定△DEF≌△BCF;
(2)由已知知△ABD是直角三角形,由已知AD=3,BD=6,可得出∠ABD=30°,然后利用折叠的性质可得∠DBE=30°,继而可求得∠EBC的度数.
试题解析:(1)由折叠的性质可得:DE=BC,∠E=∠C=90°,
在△DEF和△BCF中,
 ,
,
∴△DEF≌△BCF(AAS);
(2)在Rt△ABD中,
∵AD=3,BD=6,
∴∠ABD=30°,
由折叠的性质可得;∠DBE=∠ABD=30°,
∴∠EBC=90°﹣30°﹣30°=30°.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
