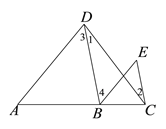
题目内容
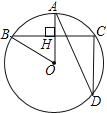
【题目】如图,在⊙O中,半径OA⊥弦BC于点H,点D在优弧BC上
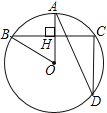
(1)若∠AOB=50°,求∠ADC的度数;
(2)若BC=8,AH=2,求⊙O的半径.
【答案】
【解析】(1)∠ADC=25°;(2)⊙O的半径为5.
试题分析:(1)根据垂径定理可得![]() =
=![]() ,再根据圆周角定理可得∠ADC=
,再根据圆周角定理可得∠ADC=![]() ∠AOB,进而可得答案;
∠AOB,进而可得答案;
(2)根据垂径定理可得BH=4,设HO=x,则AO=BO=x+2,在Rt△BHO中利用勾股定理可得(x+2)2=x2+42,解方程可得x的值,从而可得答案.
解:(1)∵半径OA⊥弦BC于点H,
∴![]() =
=![]() ,
,
∴∠ADC=![]() ∠AOB,
∠AOB,
∵∠AOB=50°,
∴∠ADC=25°;
(2)∵半径OA⊥弦BC于点H,
∴BH=![]() BC,
BC,
∵BC=8,
∴BH=4,
设HO=x,则AO=BO=x+2,
在Rt△BHO中,BO2=HO2+BH2,
∴(x+2)2=x2+42,
解得:x=3,
∴AO=5.
答:⊙O的半径为5.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目