题目内容
如图，Rt△ABC的斜边AB=10，sinA=| 3 | 5 |
（1）用尺规作图作线段AB的垂直平分线l（保留作图痕迹，不要求写作法、证明）；
（2）求直线l被Rt△ABC截得的线段长．
分析：（1）根据线段垂直平分线的作法即可得出答案，如图；
（2）根据三角函数可得出BC=6，AC=8，设直线l与AC，AB的交点为D，E，根据tanA=
，从而可得出DE的长．
（2）根据三角函数可得出BC=6，AC=8，设直线l与AC，AB的交点为D，E，根据tanA=
| 3 |
| 4 |
解答：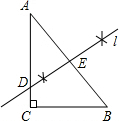
解：（1）如图：
（2）∵AB=10，sinA=
．
∴
=
，
∴BC=6，
∴AC=8，
∴tanA=
．
∵l是AB的垂直平分线，
∴AE=5，
∴
=
，
∴DE=
，
∴直线l被Rt△ABC截得的线段长为
．
解：（1）如图：（2）∵AB=10，sinA=
| 3 |
| 5 |
∴
| BC |
| AB |
| 3 |
| 5 |
∴BC=6，
∴AC=8，
∴tanA=
| 3 |
| 4 |
∵l是AB的垂直平分线，
∴AE=5，
∴
| DE |
| AE |
| 3 |
| 4 |
∴DE=
| 15 |
| 4 |
∴直线l被Rt△ABC截得的线段长为
| 15 |
| 4 |
点评：本题考查了解直角三角形以及线段垂直平分线的性质，考查了学生的作图能力，是基础题难度不大．
练习册系列答案
开心蛙口算题卡系列答案
相关题目
如图，Rt△ABC的直角边BC在x轴正半轴上，斜边AC边上的中线BD反向延长线交y轴负半轴于E，双曲线
如图，Rt△ABC的两直角边分别为1，2，以Rt△ABC的斜边AC为一直角边，另一直角边为1画第二个△ACD；在以△ACD的斜边AD为一直角边，另一直角边长为1画第三个△ADE；…，依此类推，第n个直角三角形的斜边长是
如图，Rt△ABC的斜边AB=10cm，
如图，Rt△ABC的一条直角边AB是⊙O的直径，AB=8，斜边交⊙O于D，∠A=30°，求阴影部分的面积．