题目内容
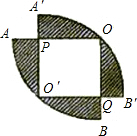 如图,两个半径为1,圆心角为90°的扇形OAB和扇形O′A′B′叠放在一起,点O′在弧AB上,四边形OPO′Q是正方形,则阴影部分的面积等于( )
如图,两个半径为1,圆心角为90°的扇形OAB和扇形O′A′B′叠放在一起,点O′在弧AB上,四边形OPO′Q是正方形,则阴影部分的面积等于( )分析:根据题意可知,正方形OPO′Q的面积是
,圆心角是90°的扇形OAB和扇形0′A′B′相等为
,所以阴影部分的面积等于
×2-2×
=
-1.
| 1 |
| 2 |
| π |
| 4 |
| π |
| 4 |
| 1 |
| 2 |
| π |
| 2 |
解答: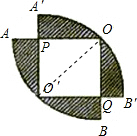 解:连接OO′,则OO′=1,
解:连接OO′,则OO′=1,
∵四边形OPO′Q是正方形,
∴OQ=O′Q,
在直角三角形OO′Q中,根据勾股定理得:
∴OQ2+O′Q2=OO′2,即2OQ2=OO′2=1,
∴OQ=
,
∴S正方形POQO=(
)2=
,
阴影部分的面积等于
×2-2×
=
-1.
故选A.
 解:连接OO′,则OO′=1,
解:连接OO′,则OO′=1,∵四边形OPO′Q是正方形,
∴OQ=O′Q,
在直角三角形OO′Q中,根据勾股定理得:
∴OQ2+O′Q2=OO′2,即2OQ2=OO′2=1,
∴OQ=
| ||
| 2 |
∴S正方形POQO=(
| ||
| 2 |
| 1 |
| 2 |
阴影部分的面积等于
| 90π×12 |
| 360 |
| 1 |
| 2 |
| π |
| 2 |
故选A.
点评:此题主要考查阴影部分面积的求法.求不规则的图形的面积,可以转化为几个规则图形的面积的和或差来求.本题的解题关键是阴影部分的面积是扇形OAB和扇形0′A′B面积和减去2个正方形OPO′Q的面积的差.

练习册系列答案
相关题目
 如图,两个半径为2cm的等圆互相重叠,且各自的圆心都在另一个圆上,则两圆重叠部分的面积是
如图,两个半径为2cm的等圆互相重叠,且各自的圆心都在另一个圆上,则两圆重叠部分的面积是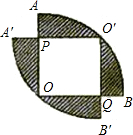 如图,两个半径为1,圆心角是90°的扇形OAB和扇形0′A′B′,叠放在一起,点0′在
如图,两个半径为1,圆心角是90°的扇形OAB和扇形0′A′B′,叠放在一起,点0′在
 (1)如图,两个半径为1的圆有一部分互相重叠,其重叠部分的面积是其中一个圆的面积的
(1)如图,两个半径为1的圆有一部分互相重叠,其重叠部分的面积是其中一个圆的面积的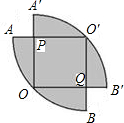 如图,两个半径为1的
如图,两个半径为1的