Question

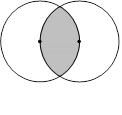
如图，两个半径为1的

1

4

圆扇形A′OB′与AO′B叠放在一起，POQO'是正方形，则整个阴影图形的面积是

 

．

Answer 1

分析：连OO′，由OO′=1，得到正方形边长OP=

2

2

OO′=

2

2

；再由S_阴影部分=S_{扇形OA′B′}+S_扇形O′AB-S_{正方形OPO′Q}，根据扇形的面积公式进行计算即可．

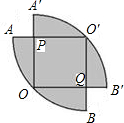
解答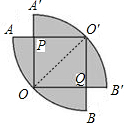：解：连OO′，如图，
则OO′=1，
∴OP=

2

2

OO′=

2

2

；
∴S_阴影部分=S_{扇形OA′B′}+S_扇形O′AB-S_{正方形OPO′Q}=2×

90π×12

360

-（

2

2

）²=

π-1

2

．
故答案为

π-1

2

．

点评：本题考查了扇形的面积公式：S=

nπR2

360

，其中n为扇形的圆心角的度数，R为圆的半径），或S=

1

2

lR，l为扇形的弧长，R为半径．也考查了正方形的性质．