题目内容
如图，两个半径为2cm的等圆互相重叠，且各自的圆心都在另一个圆上，则两圆重叠部分的面积是分析：连接相交两圆的交点，根据其图形的对称性可知，阴影部分的面积等于公共弦与圆所构成的弓形面积的2倍．
解答：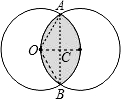
解：如图连接AB，OA、OB，
根据对称性可知OA=OB=2，OC⊥AB，OC=1，
∴∠AOB=2∠AOC=2×60°=120°，
∴S阴影部分=2（S扇形AOB-S△AOB）
=2（
-
）
=（
π-2
）
故答案为：（
π-2
）．
解：如图连接AB，OA、OB，根据对称性可知OA=OB=2，OC⊥AB，OC=1，
∴∠AOB=2∠AOC=2×60°=120°，
∴S阴影部分=2（S扇形AOB-S△AOB）
=2（
| 120π×22 |
| 360 |
| 3 |
=（
| 8 |
| 3 |
| 3 |
故答案为：（
| 8 |
| 3 |
| 3 |
点评：本题考查了扇形的面积及相交两圆的性质，解题的关键是正确的分析图形并分解为两个弓形的面积的和．
练习册系列答案
相关题目
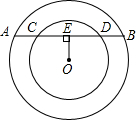如图，两个同心圆中，大圆的弦AB交小圆与点C、D，OE⊥AB垂足为E，且OE=1，若AB=4，CD=2，则两个同心圆的半径之比为（ ）| A、3：2 | ||||
B、
| ||||
C、
| ||||
| D、2：1 |
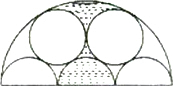如图，两个圆与三个半圆彼此相切，它们的半径都是1单位，并且它们又都与一个大半圆相切，则阴影部分的面积为（ ）| A、π | ||
B、
| ||
C、
| ||
D、
|
如图，两个半径相等的直角扇形的圆心分别在对方的圆弧上，半径AE、CF交于点G，半径BE、CD交于点H，且点C是弧AB的中点，若扇形的半径为2，则图中阴影部分的面积等于（ ）| A、π+4 | B、2π-2 | C、2π-4 | D、π-1 |
如图，两个半径相等的直角扇形的圆心分别在对方的圆弧上，半径AE、CF交于点G，半径BE、CD交于点H，且点C是弧AB的中点，若扇形的半径为2，则图中阴影部分的面积等于