题目内容
【题目】如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=2:3.其中正确结论的个数是( ) 
A.4个
B.3个
C.2个
D.1个
【答案】B
【解析】解:①∵矩形ABCD中,O为AC中点,
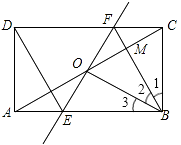
∴OB=OC,
∵∠COB=60°,
∴△OBC是等边三角形,
∴OB=BC,
∵FO=FC,
∴FB垂直平分OC,
故①正确;
②∵△BOC为等边三角形,FO=FC,
∴BO⊥EF,BF⊥OC,
∴∠CMB=∠EOB=90°,
∴BO≠BM,
∴△EOB与△CMB不全等;
故②错误;
③易知△ADE≌△CBF,∠1=∠2=∠3=30°,
∴∠ADE=∠CBF=30°,∠BEO=60°,
∴∠CDE=60°,∠DFE=∠BEO=60°,
∴∠CDE=∠DFE,
∴DE=EF,
故③正确;
④易知△AOE≌△COF,
∴S△AOE=S△COF,
∵S△COF=2S△CMF,
∴S△AOE:S△BCM=2S△CMF:S△BCM= ![]() ,
,
∵∠FCO=30°,
∴FM= ![]() ,BM=
,BM= ![]() CM,
CM,
∴ ![]() =
= ![]() ,
,
∴S△AOE:S△BCM=2:3,
故④正确;
所以其中正确结论的个数为3个;
故选B
①利用线段垂直平分线的性质的逆定理可得结论;②在△EOB和△CMB中,对应直角边不相等,则两三角形不全等;③可证明∠CDE=∠DFE;④可通过面积转化进行解答.

练习册系列答案
相关题目