��Ŀ����
����Ŀ����֪����ͼ�٣���ƽ��ֱ������ϵxOy�У�A��0��5����C��![]() ��0����AOCDΪ���Σ�AE��ֱ�ڶԽ���OD��E����F�ǵ�E����y��ĶԳƵ㣬��AF��OF��
��0����AOCDΪ���Σ�AE��ֱ�ڶԽ���OD��E����F�ǵ�E����y��ĶԳƵ㣬��AF��OF��
��1����AF��OF�ij���
��2����ͼ�ڣ�����OAF�Ƶ�O˳ʱ����תһ���Ǧ���0�㣼����180�㣩������ת�еġ�OAFΪ��OA��F�䣬����ת�����У���A��F�����ڵ�ֱ�����߶�AD���ڵ�P�����߶�OD���ڵ�Q���Ƿ����������P��Q���㣬ʹ��DPQΪ���������Σ������ڣ������ʱ��P���ꣻ�������ڣ���˵�����ɣ�

���𰸡���1��AF=4��OF=3����2�����ڣ���P������Ϊ����![]() ��5������
��5������![]() ��
��![]() ��5��
��5��
�������������������1�����ù��ɶ����������ȷ������Գ����ʼ�����⣻
��2������ͼ�Σ�����PQ=PD��PD=DQ���ƽ���ߵ����ʣ��Զ�����Ⱥͽǵĵ������������ù��ɶ���������⣮
�⣺��1����ͼ��
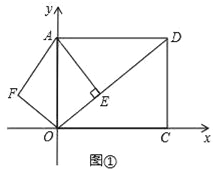
��OA=5��AD=OC=![]() ��
��
�ɹ��ɶ�������OD=![]() ��
��
��AE��OD=AO��AD��
��AE=4��
��OE=![]() =3��
=3��
�ߵ�F�ǵ�E����y��ĶԳƵ㣬
��AF=AE=4��OF=OE=3��
��2����ͼ��
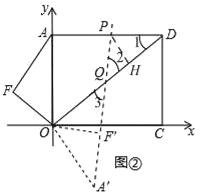
��PD=PQ��
�á�1=��2=��3��
�ߡ�1=��A�䣬
���3=��A�䣬
��OQ=OA��=5��
��DQ=![]() ��
��
����P��PH��DQ��
��![]() ��
��
��cos��1=![]() ��
��
��DP=![]() ��
��
��AP=![]() ��
��
���ʱ��P������Ϊ��![]() ��5����
��5����
��ͼ��
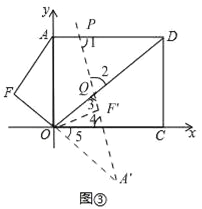
�ߵ�P���߶�AD�ϣ�
���1����PDQ��
��QP��QD������ȣ�
��ͼ�ۣ�
��DP=DQ��
���1=��2=��3=��4��
�ߡ�3=��5+��A�䣬��A��=��COD��
���4=��A��OQ��
��A��Q=A��O=5��
��F��Q=5��4=1��
��OQ=![]() ��
��
��DP=DQ=![]() ��
��![]() ��
��
��AP=AD��DP=![]() ��
��![]() ��
��
���ʱ��P������Ϊ����![]() ��
��![]() ��5����
��5����

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�