题目内容
(1)计算:(1+
)2(1+
)2(1-
)2(1-
)2;
(2)已知1<x<2,化简:
+
.
| 2 |
| 3 |
| 2 |
| 3 |
(2)已知1<x<2,化简:
| 4-4x+x2 |
| x2+2x+1 |
考点:二次根式的混合运算,二次根式的性质与化简
专题:计算题
分析:(1)根据积的乘方得到原式=[(1+
)(1-
)]2•[(1+
)(1-
)]2,然后利用平方差公式计算;
(2)先根据二次根式的性质化简得到原式=|x-2|+|x+1|,然后根据x的取值范围去绝对值后合并即可.
| 2 |
| 2 |
| 3 |
| 3 |
(2)先根据二次根式的性质化简得到原式=|x-2|+|x+1|,然后根据x的取值范围去绝对值后合并即可.
解答:解:(1)原式=[(1+
)(1-
)]2•[(1+
)(1-
)]2
=(1-2)2×(1-3)2
=1×4
=4;
(2)∵1<x<2,
∴原式=
+
=|x-2|+|x+1|
=-(x-2)+x+1
=-x+2+x+1
=3.
| 2 |
| 2 |
| 3 |
| 3 |
=(1-2)2×(1-3)2
=1×4
=4;
(2)∵1<x<2,
∴原式=
| (x-2)2 |
| (x+1)2 |
=|x-2|+|x+1|
=-(x-2)+x+1
=-x+2+x+1
=3.
点评:本题考查了二次根式的混合运算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.

练习册系列答案
相关题目
下列说法中正确的是( )
| A、3是-27的立方根 |
| B、(-2)3的立方根是-2 |
| C、4的平方根是2 |
| D、25的算术平方根是-5 |
用字母a表示任意一个有理数,下列四个代数式中,值不可能为0的是( )
| A、1+|a| |
| B、|a+1| |
| C、a2 |
| D、a3+1 |
某抛物线的顶点坐标为(1,-2),且经过(2,1),则抛物线的解析式为( )
| A、y=3x2-6x-5 |
| B、y=3x2-6x+1 |
| C、y=3x2+6x+1 |
| D、y=3x2+6x+5 |
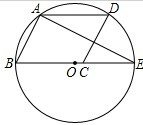 如图,平行四边形ABCD的顶点A、B、D在⊙O上,顶点C在⊙O的直径BE上,∠ADC=52°,连接AE,则∠AEB的度数为( )
如图,平行四边形ABCD的顶点A、B、D在⊙O上,顶点C在⊙O的直径BE上,∠ADC=52°,连接AE,则∠AEB的度数为( )| A、26° | B、38° |
| C、48° | D、64° |