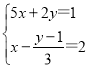题目内容
【题目】在平面直角坐标系xOy中,直线AB:y=-x+b分别与x、y轴交于A(3,0)、B两点.

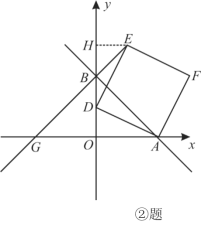
(1)如图,求点B的坐标;
(2)点D为线段OB上的动点(点D不与点O重合),以AD为边,在第一象限内作正方形ADEF.
①如图,设点D为(0,m),请用含m的代数式表示点F的坐标;
②如图,连结EB并延长交x轴于点G.当D点运动时,G点的位置是否发生变化?如果不变,请求出G点的坐标;如果变化,请说明理由.
【答案】(1)(0,3);(2)①F(m+3,3) ,②不变,(-3,0)
【解析】
(1)要求B点坐标,得先求函数表达式,然后代入求值即可.
(2)①根据题意作图,由正方形的性质证明出△DOA≌△AMF,用m表示各边长,即可表示出点F的坐标.
②过E作EH⊥x轴于H,由正方形的性质证明出△HDE≌△OAD,进而证出△BHE是等腰直角三角形,即证出△BOG为等腰直角三角形即得到结果.
解: (1)把A(3,0)坐标代入直线AB解析式y=-x+b,
得0=-3+b,
解得:b=3,
∴ 直线AB的解析式为y=-x+3,
当x=0时,y=3,
∴ 点B的坐标是(0,3);
(2)①过F作FM⊥x轴于M,则∠AMF=∠AOD=90°,
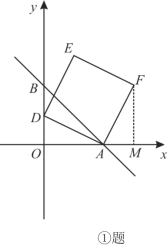
∵ 四边形ADEF正方形,
∴ AD=AF,∠DAF=90°,
∴ ∠DAO+∠FAM=90°,∠AFM+∠FAM=90°,
∴ ∠DAO=∠AFM,
∴ △DOA≌△AMF,
∴ FM=OA=3,AM=OD=m,
∴ OM=m+3,
∴ F(m+3,3) ;
② G点位置不变,坐标为:G(-3,0),
过E作EH⊥x轴于H则∠EHD=∠DOA=90°,
∵ 四边形ADEF正方形,
∴ AD=DE,∠ADE=90°,
∴ ∠ADO+∠HDE=90°,∠ADO+∠DAO=90°,
∴ ∠HDE=∠OAD,
∴ △HDE≌△OAD
∴ HE=OD,OA=DH,
∵ OA=OB,
∴ DH=OB,
∴ DH-BD=BO-BD,
即:BH=OD,
又HE=OD,
∴ BH=HE,
∴ △BHE是等腰直角三角形,
∴ ∠HBE=45°,
∴ ∠OBG=45°,
∴ △BOG为等腰直角三角形,
∴ OG=OB=3,
∴ G(-3,0).
方法二:同方法一先证△HDE≌△OAD ,
∴ HE=OD=m,OA=DH=3,
∴ E(m,m+3),
∵ B(0,3),
设直线BE的解析式为y=kx+b
则∵ m>0,
∴k=1,
∴ 直线BE的解析式为y=x+3,
当y=0时,x=-3,
∴ 点G的位置不变,坐标为(-3,0).