题目内容
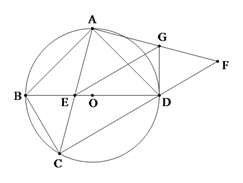
【题目】如图,在△ABC中,∠ACB=90°,点O在AC上,以O为圆心,OC为半径作⊙O,过点A作AD⊥BO交BO的延长线于点D.则下列结论中:①点A、B、C、D在同一个圆上;②∠ABC=2∠CAD;③若∠BOC=∠BAD,则AB与⊙O相切,正确的结论是( )
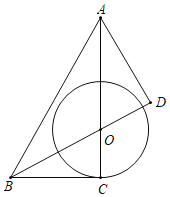
A.①②③B.①②C.②③D.①③
【答案】D
【解析】
由∠D=90°=∠ACB,得出点A、B、C、D在同一个圆上,①正确;证出∠OBC=∠CAD,当BD是∠ABC平分线时,∠ABC=2∠CAD,②错误;若∠BOC=∠BAD,则∠OBC=∠ABD,作OE⊥AB于E,由角平分线性质得出OE=OC,得出AB与⊙O相切,③正确;即可得出结论.
解:∵AD⊥BO,
∴∠D=90°=∠ACB,
∴点A、B、C、D在同一个圆上,①正确;
∵∠ACB=∠D=90°,∠BOC=∠AOD,
∴∠OBC=∠CAD,
当BD是∠ABC平分线时,∠ABC=2∠CAD,②错误;
若∠BOC=∠BAD,
∵∠ACB=∠D=90°,
∴∠OBC=∠ABD,
作OE⊥AB于E,如图所示:
则OE=OC,
∴AB与⊙O相切,③正确;
故选:D.
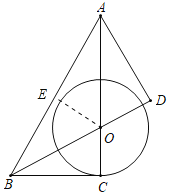

练习册系列答案
相关题目