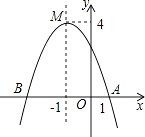题目内容
【题目】如图,在平面直角坐标系xoy中,椭圆 ![]() 的右顶点和上顶点分别为点A,B,M是线段AB的中点,且
的右顶点和上顶点分别为点A,B,M是线段AB的中点,且 ![]() ..
.. 
(1)求椭圆的离心率;
(2)若a=2,四边形ABCD内接于椭圆,AB∥CD,记直线AD,BC的斜率分别为k1 , k2 , 求证:k1k2为定值.
【答案】
(1)解:A(a,0),B(0,b),线段AB的中点M ![]() .
.
![]() =(﹣a,b),
=(﹣a,b), ![]() =
= ![]() .
.
∵ ![]() .
.
∴ ![]() +
+ ![]() =﹣
=﹣ ![]() b2,化为:a=2b.
b2,化为:a=2b.
∴椭圆的离心率e= ![]() =
= ![]() =
= ![]()
(2)解:证明:由a=2,可得b=1,
∴椭圆的标准方程为: ![]() +y2=1,A(2,0),B(0,1).
+y2=1,A(2,0),B(0,1).
直线BC的方程为:y=k2x+1,联立  ,化为:(1+
,化为:(1+ ![]() )x2+8k2x=0,
)x2+8k2x=0,
解得xC= ![]() ,∴yC=
,∴yC= ![]() .即C(
.即C( ![]() ,
, ![]() ).
).
直线AD的方程为:y=k1(x﹣2),联立  ,化为:
,化为: ![]() x2﹣16
x2﹣16 ![]() x+
x+ ![]() ﹣4=0,
﹣4=0,
∴2xD= ![]() ,解得xD=
,解得xD= ![]() ,yD=
,yD= ![]() ,可得D(
,可得D( ![]() ,
, ![]() )
)
∴kCD= ![]() =﹣
=﹣ ![]() ,
,
化为:1﹣16 ![]() +2k1﹣2k2+8
+2k1﹣2k2+8 ![]() ﹣8
﹣8 ![]() =0.
=0.
∴ ![]() (4k1k2+4k1﹣4k2+1)=0,
(4k1k2+4k1﹣4k2+1)=0,
∴k1k2= ![]() .
.
【解析】(1)A(a,0),B(0,b),线段AB的中点M ![]() .利用
.利用 ![]() 与离心率的计算公式即可得出.(2)由a=2,可得b=1,可得椭圆的标准方程为:
与离心率的计算公式即可得出.(2)由a=2,可得b=1,可得椭圆的标准方程为: ![]() +y2=1,A(2,0),B(0,1).直线BC的方程为:y=k2x+1,直线AD的方程为:y=k1(x﹣2),分别于同一方程联立解得C,D,坐标,利用kCD=
+y2=1,A(2,0),B(0,1).直线BC的方程为:y=k2x+1,直线AD的方程为:y=k1(x﹣2),分别于同一方程联立解得C,D,坐标,利用kCD= ![]() =﹣
=﹣ ![]() ,即可得出.
,即可得出.

【题目】函数y=x2+3x+2的图象如图1所示,根据图象回答问题: 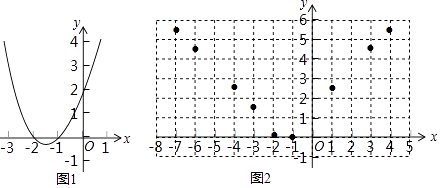
(1)当x时,x2+3x+2>0;
(2)在上述问题的基础上,探究解决新问题: ①函数y= ![]() 的自变量x的取值范围是;
的自变量x的取值范围是;
②如表是函数y= ![]() 的几组y与x的对应值.
的几组y与x的对应值.
x | … | ﹣7 | ﹣6 | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 3 | 4 | … |
y | … | 5.477… | 4.472… | 2.449… | 1.414… | 0 | 0 | 1.414… | 2.449… | 4.472… | 5.477… | … |
如图2,在平面直角坐标系xOy中,描出了上表中各对对应值为坐标的点的大概位置,请你根据描出的点,画出该函数的图象:
③写出该函数的一条性质: .