Question

【题目】如图，是方城县潘河的某一段，现要测量河的宽度（即河两岸相对的两点A、B间的距离），先在AB的垂线BF上取两点C、D，使BC＝CD，再定出BF的垂线DE，使点A、C、E在同一条直线上，直接在河岸上测量DE的长度就知道河的宽度AB了，你知道这是为什么吗？请先判断DE和AB大小关系，然后说明理由.

Answer 1

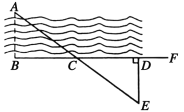
【答案】AB＝DE，理由见解析.

【解析】

首先由BF⊥AB，DE⊥BD，可得∠ABC＝∠CDE＝90°，再由条件BC＝CD，∠ACB＝∠ECD，利用ASA证出△ABC≌△EDC，根据全等三角形对应边相等可得到AB＝DE．

解：AB＝DE，

理由：∵BF⊥AB，DE⊥BD，

∴∠ABC＝∠CDE＝90°，

在△ABC和△EDC中，，

∴△ABC≌△EDC（ASA），

∴AB＝DE，

∴在河岸上测量DE的长度就知道河的宽度AB了.