Question

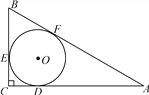
【题目】如图，⊙O为△ABC的内切圆，切点分别为D，E，F，∠C＝90°，BC＝3，AC＝4.

(1)求△ABC的面积；

(2)求⊙O的半径；

(3)求AF的长．

Answer 1

【答案】(1) 6；(2)⊙O的半径为1；(3) 3

【解析】(1)、已知了直角三角形的两条直角边，可根据直角三角形的面积公式求出△ABC的面积；(2)、连接OE、OD，则OE、OD即为所求的半径；易证得四边形OECD是正方形，那么CE、CD都等于⊙O的半径，可用⊙O的半径分别表示出BE、AD的长，由切线长定理知BE=BF、AD=AF，即可由BF+AF=AB=5求出⊙O的半径；(3)、求得⊙O的半径后，即可求出AD的值，而AF=AD，由此得解．

(1)、∵∠C＝90°，BC＝3，AC＝4， ∴S△ABC＝×3×4＝6；

(2)、如答图，连结OE，OD，OF.

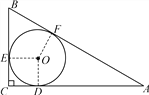
∵⊙O为△ABC的内切圆，D，E，F为切点， ∴EB＝FB，CD＝CE，AD＝AF，OE⊥BC，OD⊥AC.

又∵∠C＝90°，OD＝OE， ∴四边形ECDO为正方形， 设OE＝OD＝CE＝CD＝x，

则EB＝3－x，AD＝4－x，FB＝3－x，AF＝4－x. 又∵AB＝＝5，∴3－x＋4－x＝5，

解得x＝1.即⊙O的半径为1；

(3)∵CD＝1，∴AF＝AD＝4－1＝3.