题目内容
函数y=x2+4x+3的图象开口向________，当x________时，y的值随着x的值增大而增大；当x________时，y的值随着x的值增大而减小．
上 x＞-2 ＜-2
分析：根据二次函数的性质，找到解析式中的a、b、c分别为1、4、3；由a的值可判断出开口方向，利用对称轴公式求出对称轴方程，在对称轴的两侧可以讨论函数的增减性．
解答：在y=x2+4x+3中，a=1，b=4，c=3，
∵a＞0，
∴开口向上，
由于函数的对称轴为x=-
=-2，
当x＜-2时，y的值随着x的值增大而减小；
当x＞-2时，y的值随着x的值增大而增大．
故答案为：上，x＞-2，x＜-2．
点评：本题考查了二次函数的性质，找到一般式中的a、b、c，求出对称轴是解题的关键．
分析：根据二次函数的性质，找到解析式中的a、b、c分别为1、4、3；由a的值可判断出开口方向，利用对称轴公式求出对称轴方程，在对称轴的两侧可以讨论函数的增减性．
解答：在y=x2+4x+3中，a=1，b=4，c=3，
∵a＞0，
∴开口向上，
由于函数的对称轴为x=-
=-2，当x＜-2时，y的值随着x的值增大而减小；
当x＞-2时，y的值随着x的值增大而增大．
故答案为：上，x＞-2，x＜-2．
点评：本题考查了二次函数的性质，找到一般式中的a、b、c，求出对称轴是解题的关键．
练习册系列答案
相关题目
，点N是x轴负半轴上的一点，NH⊥CM，交CM（或CM的延长线）于点H，交y轴于点D，且ND=CM．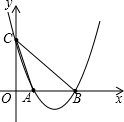
如图，已知二次函数y=x2-4x+3的图象交x轴于A、B两点（点A在点B的左侧）抛物线y=x2-4x+3交y轴于点C．