题目内容
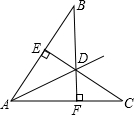 已知:如图,CE⊥AB,BF⊥AC,CE与BF相交于D,且BD=CD.求证:D在∠BAC的平分线上.
已知:如图,CE⊥AB,BF⊥AC,CE与BF相交于D,且BD=CD.求证:D在∠BAC的平分线上.
分析:首先根据已知条件易证△BDE≌△CDF(AAS),则DE=DF,再由角平分线性质的逆定理可得D在∠BAC的平分线上.
解答:证明:在△BDE和△CDF中,
∵
,
∴△BDE≌△CDF(AAS),
∴DE=DF,
又∵CE⊥AB,BF⊥AC,
∴D在∠BAC的平分线上.
∵
|
∴△BDE≌△CDF(AAS),
∴DE=DF,
又∵CE⊥AB,BF⊥AC,
∴D在∠BAC的平分线上.
点评:此题主要考查角平分线性质的逆定理,首先证明Rt△BDE≌Rt△CDF,是关键.

练习册系列答案
相关题目
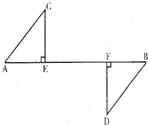 24、已知:如图,CE⊥AB,DF⊥AB,垂足分别为E、F,AC∥DB,且AE=FB.
24、已知:如图,CE⊥AB,DF⊥AB,垂足分别为E、F,AC∥DB,且AE=FB. 17、已知:如图,CE⊥AB,DF⊥AB,AF=BE,CE=DF.
17、已知:如图,CE⊥AB,DF⊥AB,AF=BE,CE=DF.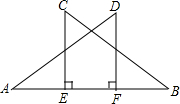 已知:如图,CE⊥AB,DF⊥AB,CE=DF,BC=AD,则△CEB≌△DFA吗?说明理由.
已知:如图,CE⊥AB,DF⊥AB,CE=DF,BC=AD,则△CEB≌△DFA吗?说明理由. 已知:如图,CE是△ABC的一个外角平分线,且EF∥BC交AB于F点,∠A=60°,∠CEF=55°,求∠EFB的度数.
已知:如图,CE是△ABC的一个外角平分线,且EF∥BC交AB于F点,∠A=60°,∠CEF=55°,求∠EFB的度数.