题目内容
 已知:如图,CE是△ABC的一个外角平分线,且EF∥BC交AB于F点,∠A=60°,∠CEF=55°,求∠EFB的度数.
已知:如图,CE是△ABC的一个外角平分线,且EF∥BC交AB于F点,∠A=60°,∠CEF=55°,求∠EFB的度数.分析:根据两直线平行,内错角相等求出∠ECD=∠CEF,再根据角平分线的定义求出∠ACD,然后根据三角形的一个外角等于与它不相邻的两个内角的和求出∠B,再根据两直线平行,同旁内角互补求解即可.
解答:解:∵EF∥BC,∠CEF=55°,
∴∠ECD=∠CEF=55°,
∵CE是△ABC的一个外角平分线,
∴∠ACD=2∠ECD=2×55°=110°,
∵∠A=60°,
∴∠B=∠ACD-∠A=110°-60°=50°,
∵EF∥BC,
∴∠EFB=180°-∠B=180°-50°=130°.
∴∠ECD=∠CEF=55°,
∵CE是△ABC的一个外角平分线,
∴∠ACD=2∠ECD=2×55°=110°,
∵∠A=60°,
∴∠B=∠ACD-∠A=110°-60°=50°,
∵EF∥BC,
∴∠EFB=180°-∠B=180°-50°=130°.
点评:本题考查了平行线的性质,三角形的角平分线的定义,是基础题,熟记性质是解题的关键.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
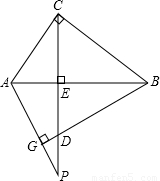
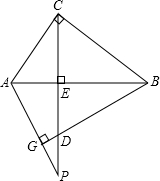 已知:如图,CE是Rt△ABC的斜边AB上的高,BG⊥AP.求证:CE2=ED•EP.
已知:如图,CE是Rt△ABC的斜边AB上的高,BG⊥AP.求证:CE2=ED•EP.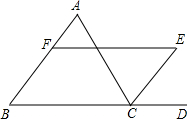 已知:如图,CE是△ABC的一个外角平分线,且EF∥BC交AB于F点,∠A=60°,∠CEF=55°,求∠EFB的度数.
已知:如图,CE是△ABC的一个外角平分线,且EF∥BC交AB于F点,∠A=60°,∠CEF=55°,求∠EFB的度数.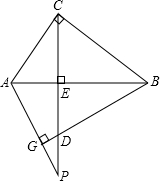 已知:如图,CE是Rt△ABC的斜边AB上的高,BG⊥AP.求证:CE2=ED•EP.
已知:如图,CE是Rt△ABC的斜边AB上的高,BG⊥AP.求证:CE2=ED•EP.